Hierarchical Clustering¶
As you may know, clustering is an unsupervised machine learning technique that groups similar data points together based on certain features. The goal is to segregate groups with similar traits and assign them into clusters.
In this article we will implement some clustering techniques on a biology dataset based on this paper here
What is Hierarchical Clustering¶
Hierarchical clustering is a method in unsupervised learning that groups alike items into clusters. It forms a chain of clusters by either combining or dividing them based on how similar they are.
This technique organizes similar items into a structure called a dendrogram. Starting with each data item as an individual cluster, it progressively merges clusters that are alike. This results in a branching structure that illustrates the connections and hierarchies among clusters.
The dendrogram produced by hierarchical clustering showcases the layered nature of clusters, emphasizing the inherent groupings present in the data. This visual display of cluster relationships aids in spotting trends and anomalies, making it valuable for initial data exploration.
Type of Hierarchical Clustering¶
There are two types of hierarchical clustering:
- Agglomerative: This is a "bottom-up" approach. Start with many small clusters and merge them together to create bigger clusters.
- Divisive: This is a "top-down" approach. Start with a single cluster and divide it into smaller clusters.
You can see on the picture below :
Read a Dendrogram¶
A dendrogram is a tree-like diagram that displays the sequence in which clusters are formed in hierarchical clustering. It's a visual representation of the hierarchical clustering process.
How to read a Dendrogram:
Y-axis: Represents the distance (or dissimilarity) at which the clusters merged. The higher the merge point on the Y-axis, the less similar the merged clusters are.X-axis: Represents the data points or clusters.
Create a Dendrogram¶
We can build the Dendrogram with the two methods Agglomerative or Divisive. Agglomerative clustering is generally the preferred method in the litterature. Let's explore the Agglomerative method or start at the bottom method. Each data point is treated as a single cluster, so if there are N data points, there are N clusters.
As you move up the Y-axis, clusters merge based on the mininmum distance between them. A horizontal line represents where two clusters merge. The height of the horizontal line (on the Y-axis) shows the distance at which the two clusters merged.
This process continues until all data points are merged into a single cluster at the top.
Cutting a Dendrogram¶
To decide the number of clusters to consider, you can "cut" the dendrogram horizontally. The number of vertical lines the cut line passes is the number of clusters. For example in the picture above we have 4 clusters.
Linkage Criteria¶
The linkage criterion determines the distance between two clusters based on their individual data points. This distance is used to decide which clusters should be merged at each step of the hierarchical clustering they are :
- Single Linkage: Minimum pairwise distance. It considers the shortest distance between the two clusters.
- Complete Linkage: Maximum pairwise distance. It considers the longest distance between the two clusters.
- Average Linkage: Average pairwise distance.
- Centroid Linkage: Distance between the centroids of the clusters.
- Ward’s Linkage: Minimize the variance in the distances between clusters.
For a same dataset it can leads to very differents result as you can see below :
Applications¶
Hierarchical clustering has numerous practical uses in various fields. Some examples are:
- Bioinformatics: Classifying animals based on their biological characteristics to build evolutionary trees.
- Commerce: Segmenting customers or organizing employees in a hierarchy based on their earnings.
- Image analysis: Classifying handwritten letters in text identification by comparing the likeness of their forms.
- Information Search: Sorting search outcomes according to the search term.
Hierarchical clustering algo idea¶
Hierarchical clustering use measures of distance/similarity to define clusters. The principals steps for Agglomerative clustering can be summarized as follows:
- Step 1: Compute the proximity matrix using a particular distance metric
- Step 2: Each data point is assigned to a cluster
- Step 3: Merge the clusters based on a metric for the similarity between clusters
- Step 4: Update the distance matrix
- Step 5: Repeat Step 3 and Step 4 until only a single cluster remains
Let's explain each phases with simple example, so you can see it is not that difficult.
Step 1 - Proximity matrix¶
Proximity (or Distance) matrix is a square matrix (two-dimensional array) containing the distances, taken pairwise, between the elements of a set. Depending upon the application involved, the distance being used to define this matrix may or may not be a metric. More informations on Wikipedia
The distance into the proximity matrix can be calculated using various metrics, such as:
- Euclidean distance
- Manhattan distance
- Cosine similarity (for vectors)
- Hamming distance (for strings)
- ... and many others 😂
For a dataset with $N$ data points, the distance matrix will be of size $N×N$. Now, let's focus on a simple example in 2D with the Euclidean distance.
Euclidean distance¶
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. More information on wikipedia
It is the most common distance in 2D, for example the distance between two points $P(x_1,y_1)$ and $Q(x_2,y_2)$ is :
$$d(P, Q) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
Let's code a simple example with 6 data point in a 2D space plan with 🐍
In [19]:
Copied!
import numpy as np
import matplotlib.pyplot as plt
# Generate 6 random 2D points
np.random.seed(0) # for reproducibility
points = np.random.randint(1, 10, size=(6, 2))
print(points)
import numpy as np
import matplotlib.pyplot as plt
# Generate 6 random 2D points
np.random.seed(0) # for reproducibility
points = np.random.randint(1, 10, size=(6, 2))
print(points)
[[6 1] [4 4] [8 4] [6 3] [5 8] [7 9]]
In [20]:
Copied!
plt.figure(figsize=(6, 6))
plt.scatter(points[:, 0], points[:, 1], color='blue')
for i, point in enumerate(points):
plt.annotate(f'P{i}', (point[0] + 0.2, point[1] + 0.2))
plt.grid(True)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title('2D Data Plan')
plt.show()
plt.figure(figsize=(6, 6))
plt.scatter(points[:, 0], points[:, 1], color='blue')
for i, point in enumerate(points):
plt.annotate(f'P{i}', (point[0] + 0.2, point[1] + 0.2))
plt.grid(True)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title('2D Data Plan')
plt.show()
In [12]:
Copied!
import numpy as np
def euclidean_distance(point1, point2):
return np.sqrt(np.sum((np.array(point1) - np.array(point2))**2))
def compute_distance_matrix(points):
n = len(points)
distance_matrix = np.zeros((n, n))
for i in range(n):
for j in range(n):
distance_matrix[i][j] = euclidean_distance(points[i], points[j])
return distance_matrix
# Call the function
distance_matrix = compute_distance_matrix(points)
print(distance_matrix)
import numpy as np
def euclidean_distance(point1, point2):
return np.sqrt(np.sum((np.array(point1) - np.array(point2))**2))
def compute_distance_matrix(points):
n = len(points)
distance_matrix = np.zeros((n, n))
for i in range(n):
for j in range(n):
distance_matrix[i][j] = euclidean_distance(points[i], points[j])
return distance_matrix
# Call the function
distance_matrix = compute_distance_matrix(points)
print(distance_matrix)
[[0. 1.41421356 1. 4. 2. 4.12310563] [1.41421356 0. 2.23606798 3.16227766 3.16227766 3. ] [1. 2.23606798 0. 5. 2.23606798 5.09901951] [4. 3.16227766 5. 0. 4.47213595 1. ] [2. 3.16227766 2.23606798 4.47213595 0. 5. ] [4.12310563 3. 5.09901951 1. 5. 0. ]]
Step 2,3&4 - Cluster assignation¶
Computing the proximity matrix leads to define cluster, indeed as you may know now the data points who have the closest distance between them will be merge into a cluster 🥳
The main question in hierarchical clustering is how to calculate the distance between clusters and update the proximity matrix. There are many different approaches used to answer that question. Each approach has its advantages and disadvantages. The choice will depend on whether there is noise in the data set, whether the shape of the clusters is circular or not, and the density of the data points.
We tolk about how metrics can affect our clustering tasks let's view in detail how by coding the following distance functions :
- Single Linkage: The distance between two clusters is defined as the shortest distance between two points in each cluster.
- Complete Linkage: The distance between two clusters is defined as the longest distance between two points in each cluster.
- Average Linkage: The distance between two clusters is defined as the average distance between each point in one cluster to every point in the other cluster.
- Centroid Linkage: The distance between two clusters is the distance between the centroid for cluster A (a mean vector of length p) and the centroid for cluster B.
- Ward's Linkage: The criteria is the increment of the sum of squares (variance) after merging two clusters but it's a bit more tricky and requires a dendrogram-building algorithm so we will not be implementing this from scratch 😅
First let's define a plot_clusters() function in order to plot our dataset.
Let's assume we assign the first clusters like $P_0,P_3$ and $P_2$ are forming a cluster, and the other cluster is formed by $P_5$ and $P_4$.
In [32]:
Copied!
cluster1 = [points[0], points[3], points[2]]
cluster2 = [points[5], points[4]]
cluster1 = [points[0], points[3], points[2]]
cluster2 = [points[5], points[4]]
In [30]:
Copied!
import matplotlib.pyplot as plt
def plot_clusters(cluster1, cluster2, title="Clusters"):
plt.figure(figsize=(8, 8))
plt.scatter(*zip(*cluster1), color='blue', label='Cluster 1')
plt.scatter(*zip(*cluster2), color='red', label='Cluster 2')
plt.grid(True)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title(title)
plt.legend()
plt.show()
plot_clusters(cluster1, cluster2)
import matplotlib.pyplot as plt
def plot_clusters(cluster1, cluster2, title="Clusters"):
plt.figure(figsize=(8, 8))
plt.scatter(*zip(*cluster1), color='blue', label='Cluster 1')
plt.scatter(*zip(*cluster2), color='red', label='Cluster 2')
plt.grid(True)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title(title)
plt.legend()
plt.show()
plot_clusters(cluster1, cluster2)
Now let's write the linkage functions in order to see the effect they have on clustering
In [37]:
Copied!
# Let's define our metrics simply by their definitions
def single_linkage(cluster1, cluster2):
return np.min([euclidean_distance(p1, p2) for p1 in cluster1 for p2 in cluster2])
def complete_linkage(cluster1, cluster2):
return np.max([euclidean_distance(p1, p2) for p1 in cluster1 for p2 in cluster2])
def average_linkage(cluster1, cluster2):
avg_distance = np.mean([euclidean_distance(p1, p2) for p1 in cluster1 for p2 in cluster2])
return avg_distance
def centroid_linkage(cluster1, cluster2):
centroid1 = np.mean(cluster1, axis=0)
centroid2 = np.mean(cluster2, axis=0)
return euclidean_distance(centroid1, centroid2)
# Print all the metrics for our cluster before the visualisation
print("Single Linkage:", single_linkage(cluster1, cluster2))
print("Complete Linkage:", complete_linkage(cluster1, cluster2))
print("Average Linkage:", average_linkage(cluster1, cluster2))
print("Centroid Linkage:", centroid_linkage(cluster1, cluster2))
# Let's define our metrics simply by their definitions
def single_linkage(cluster1, cluster2):
return np.min([euclidean_distance(p1, p2) for p1 in cluster1 for p2 in cluster2])
def complete_linkage(cluster1, cluster2):
return np.max([euclidean_distance(p1, p2) for p1 in cluster1 for p2 in cluster2])
def average_linkage(cluster1, cluster2):
avg_distance = np.mean([euclidean_distance(p1, p2) for p1 in cluster1 for p2 in cluster2])
return avg_distance
def centroid_linkage(cluster1, cluster2):
centroid1 = np.mean(cluster1, axis=0)
centroid2 = np.mean(cluster2, axis=0)
return euclidean_distance(centroid1, centroid2)
# Print all the metrics for our cluster before the visualisation
print("Single Linkage:", single_linkage(cluster1, cluster2))
print("Complete Linkage:", complete_linkage(cluster1, cluster2))
print("Average Linkage:", average_linkage(cluster1, cluster2))
print("Centroid Linkage:", centroid_linkage(cluster1, cluster2))
Single Linkage: 5.0 Complete Linkage: 8.06225774829855 Average Linkage: 6.069021186274636 Centroid Linkage: 5.871304984602847
As you can see the values are very different from a linkage to an other, let's continue to explore and plot the differents metrics to see visually how they are computed 🤓
In [38]:
Copied!
# Let's modify our plot_clusters() function in order to to accept additional parameters for the line and annotation
def plot_clusters(cluster1, cluster2, line_points=None, annotation_text=None, title="Clusters"):
plt.figure(figsize=(8, 8))
plt.scatter(*zip(*cluster1), color='blue', label='Cluster 1')
plt.scatter(*zip(*cluster2), color='red', label='Cluster 2')
if line_points:
plt.plot(*zip(*line_points), color='green', linestyle='--')
plt.scatter(*zip(*line_points), color='green', s=100, zorder=5)
if annotation_text:
midpoint = ((line_points[0][0] + line_points[1][0]) / 2, (line_points[0][1] + line_points[1][1]) / 2)
plt.annotate(annotation_text, midpoint, fontsize=9, ha='center', color='green')
plt.grid(True)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title(title)
plt.legend()
plt.show()
def plot_single_linkage(cluster1, cluster2):
min_distance = float('inf')
point1, point2 = None, None
for p1 in cluster1:
for p2 in cluster2:
distance = euclidean_distance(p1, p2)
if distance < min_distance:
min_distance = distance
point1, point2 = p1, p2
annotation_text = f"Distance: {min_distance:.2f}"
plot_clusters(cluster1, cluster2, line_points=[point1, point2], annotation_text=annotation_text, title="Single Linkage method on our 2 clusters")
plot_single_linkage(cluster1, cluster2)
# Let's modify our plot_clusters() function in order to to accept additional parameters for the line and annotation
def plot_clusters(cluster1, cluster2, line_points=None, annotation_text=None, title="Clusters"):
plt.figure(figsize=(8, 8))
plt.scatter(*zip(*cluster1), color='blue', label='Cluster 1')
plt.scatter(*zip(*cluster2), color='red', label='Cluster 2')
if line_points:
plt.plot(*zip(*line_points), color='green', linestyle='--')
plt.scatter(*zip(*line_points), color='green', s=100, zorder=5)
if annotation_text:
midpoint = ((line_points[0][0] + line_points[1][0]) / 2, (line_points[0][1] + line_points[1][1]) / 2)
plt.annotate(annotation_text, midpoint, fontsize=9, ha='center', color='green')
plt.grid(True)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title(title)
plt.legend()
plt.show()
def plot_single_linkage(cluster1, cluster2):
min_distance = float('inf')
point1, point2 = None, None
for p1 in cluster1:
for p2 in cluster2:
distance = euclidean_distance(p1, p2)
if distance < min_distance:
min_distance = distance
point1, point2 = p1, p2
annotation_text = f"Distance: {min_distance:.2f}"
plot_clusters(cluster1, cluster2, line_points=[point1, point2], annotation_text=annotation_text, title="Single Linkage method on our 2 clusters")
plot_single_linkage(cluster1, cluster2)
In [40]:
Copied!
def plot_complete_linkage(cluster1, cluster2):
max_distance = float('-inf')
point1, point2 = None, None
for p1 in cluster1:
for p2 in cluster2:
distance = euclidean_distance(p1, p2)
if distance > max_distance:
max_distance = distance
point1, point2 = p1, p2
annotation_text = f"Distance: {max_distance:.2f}"
plot_clusters(cluster1, cluster2, line_points=[point1, point2], annotation_text=annotation_text, title="Complete Linkage method on our 2 clusters")
plot_complete_linkage(cluster1, cluster2)
def plot_complete_linkage(cluster1, cluster2):
max_distance = float('-inf')
point1, point2 = None, None
for p1 in cluster1:
for p2 in cluster2:
distance = euclidean_distance(p1, p2)
if distance > max_distance:
max_distance = distance
point1, point2 = p1, p2
annotation_text = f"Distance: {max_distance:.2f}"
plot_clusters(cluster1, cluster2, line_points=[point1, point2], annotation_text=annotation_text, title="Complete Linkage method on our 2 clusters")
plot_complete_linkage(cluster1, cluster2)
In [43]:
Copied!
def plot_centroid_linkage(cluster1, cluster2):
centroid1 = np.mean(cluster1, axis=0)
centroid2 = np.mean(cluster2, axis=0)
distance = euclidean_distance(centroid1, centroid2)
annotation_text = f"Distance: {distance:.2f}"
plot_clusters(cluster1, cluster2, line_points=[centroid1, centroid2], annotation_text=annotation_text, title="Centroid Linkage method for our 2 clusters")
plot_centroid_linkage(cluster1, cluster2)
def plot_centroid_linkage(cluster1, cluster2):
centroid1 = np.mean(cluster1, axis=0)
centroid2 = np.mean(cluster2, axis=0)
distance = euclidean_distance(centroid1, centroid2)
annotation_text = f"Distance: {distance:.2f}"
plot_clusters(cluster1, cluster2, line_points=[centroid1, centroid2], annotation_text=annotation_text, title="Centroid Linkage method for our 2 clusters")
plot_centroid_linkage(cluster1, cluster2)
In [46]:
Copied!
# Redifine our function to support average method 😅
def plot_clusters(cluster1, cluster2, line_points=None, annotation_text=None, title="Clusters"):
fig, ax = plt.subplots(figsize=(8, 8))
ax.scatter(*zip(*cluster1), color='blue', label='Cluster 1')
ax.scatter(*zip(*cluster2), color='red', label='Cluster 2')
if line_points:
ax.plot(*zip(*line_points), color='green', linestyle='--')
ax.scatter(*zip(*line_points), color='green', s=100, zorder=5)
if annotation_text:
midpoint = ((line_points[0][0] + line_points[1][0]) / 2, (line_points[0][1] + line_points[1][1]) / 2)
ax.annotate(annotation_text, midpoint, fontsize=9, ha='center', color='green')
ax.grid(True)
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_title(title)
ax.legend()
return fig, ax
def plot_average_linkage(cluster1, cluster2):
distances = []
fig, ax = plot_clusters(cluster1, cluster2, title="Average Linkage")
for p1 in cluster1:
for p2 in cluster2:
distances.append(euclidean_distance(p1, p2))
ax.plot(*zip(*[p1, p2]), color='grey', linestyle='--', linewidth=0.5)
avg_distance = np.mean(distances)
ax.set_title(f"Average Linkage (Avg Distance: {avg_distance:.2f})")
plt.show()
plot_average_linkage(cluster1, cluster2)
# Redifine our function to support average method 😅
def plot_clusters(cluster1, cluster2, line_points=None, annotation_text=None, title="Clusters"):
fig, ax = plt.subplots(figsize=(8, 8))
ax.scatter(*zip(*cluster1), color='blue', label='Cluster 1')
ax.scatter(*zip(*cluster2), color='red', label='Cluster 2')
if line_points:
ax.plot(*zip(*line_points), color='green', linestyle='--')
ax.scatter(*zip(*line_points), color='green', s=100, zorder=5)
if annotation_text:
midpoint = ((line_points[0][0] + line_points[1][0]) / 2, (line_points[0][1] + line_points[1][1]) / 2)
ax.annotate(annotation_text, midpoint, fontsize=9, ha='center', color='green')
ax.grid(True)
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_title(title)
ax.legend()
return fig, ax
def plot_average_linkage(cluster1, cluster2):
distances = []
fig, ax = plot_clusters(cluster1, cluster2, title="Average Linkage")
for p1 in cluster1:
for p2 in cluster2:
distances.append(euclidean_distance(p1, p2))
ax.plot(*zip(*[p1, p2]), color='grey', linestyle='--', linewidth=0.5)
avg_distance = np.mean(distances)
ax.set_title(f"Average Linkage (Avg Distance: {avg_distance:.2f})")
plt.show()
plot_average_linkage(cluster1, cluster2)
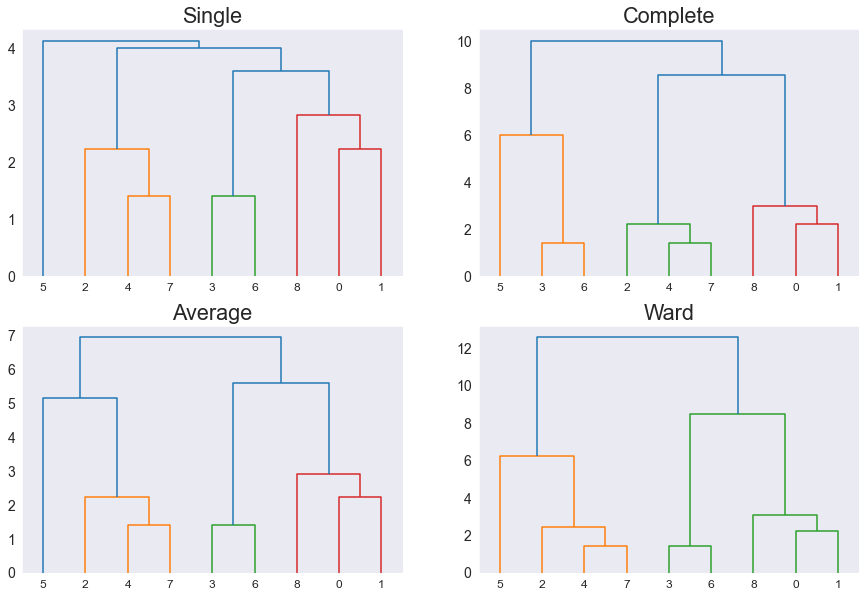
Use scipy Dendrogram¶
Now that we understand all the different metrics let's see how changing the metrics affect the final clustering and then the dendrogram. We will use the same 6 data points, so in the x-axis the number are the point number for example 0 is $P_0$. We will be using the eclidean metrics because we are in a 2D plan basically 😅
In [47]:
Copied!
from scipy.cluster.hierarchy import dendrogram, linkage
Z1 = linkage(points, method='single', metric='euclidean')
Z2 = linkage(points, method='complete', metric='euclidean')
Z3 = linkage(points, method='average', metric='euclidean')
Z4 = linkage(points, method='ward', metric='euclidean')
from scipy.cluster.hierarchy import dendrogram, linkage
Z1 = linkage(points, method='single', metric='euclidean')
Z2 = linkage(points, method='complete', metric='euclidean')
Z3 = linkage(points, method='average', metric='euclidean')
Z4 = linkage(points, method='ward', metric='euclidean')
In [48]:
Copied!
plt.figure(figsize=(15, 10))
plt.subplot(2,2,1), dendrogram(Z1), plt.title('Single')
plt.subplot(2,2,2), dendrogram(Z2), plt.title('Complete')
plt.subplot(2,2,3), dendrogram(Z3), plt.title('Average')
plt.subplot(2,2,4), dendrogram(Z4), plt.title('Ward')
plt.show()
plt.figure(figsize=(15, 10))
plt.subplot(2,2,1), dendrogram(Z1), plt.title('Single')
plt.subplot(2,2,2), dendrogram(Z2), plt.title('Complete')
plt.subplot(2,2,3), dendrogram(Z3), plt.title('Average')
plt.subplot(2,2,4), dendrogram(Z4), plt.title('Ward')
plt.show()
In [ ]:
Copied!
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
data = "/Users/mac/Downloads/Tdata_Amiens.csv"
df = pd.read_csv(data, sep=';', decimal=',', na_values='#N/A')
pd.set_option('display.max_columns', None)
df.head()
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
data = "/Users/mac/Downloads/Tdata_Amiens.csv"
df = pd.read_csv(data, sep=';', decimal=',', na_values='#N/A')
pd.set_option('display.max_columns', None)
df.head()
Out[ ]:
| Measuring_date | Round_Order | Tray_ID | Tray_Info | Position | plant_ID_treatment | plant ID 2 | Day_after_sowing | transgenic_line | treatement | Size1? | Fo | Fm | Fv | QY_max | NDVI2 | PRI | SIPI | NDVI | PSRI | MCARI1 | OSAVI | Size2? | Area_(mm2) | Slenderness | RGB(72,84,58) | RGB(73,86,36) | RGB(57,71,46) | RGB(59,71,20) | %RGB(72,84,58) | %RGB(73,86,36) | %RGB(57,71,46) | %RGB(59,71,20) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2022-04-19 | 16 | PS_Tray_1400 | E | Area 7 | MD5 | FC5 1-MD544670 | 19 | FC5_1 | medium drought | 139 | 1713.968347 | 11504.69545 | 9790.727097 | 0.849128989 | 0.0747295 | -0.003369734 | 0.679499612 | 0.659085318 | 0.038718806 | 0.407859346 | 0.648309302 | 9.329418182 | 15.4287 | 1.627486438 | 32.0 | 128.0 | 61.0 | 21.0 | 5.786618445 | 23.14647378 | 11.03074141 | 3.797468354 |
| 1 | 2022-04-19 | 16 | PS_Tray_1400 | E | Area 19 | MD5 | irx14-MD544670 | 19 | irx14 | medium drought | 17 | 1428.841181 | 7899.705854 | 6470.864746 | 0.818560001 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.0 | 0.0 | 0.0 | 0.0 | #DIV/0! | #DIV/0! | #DIV/0! | #DIV/0! |
| 2 | 2022-04-19 | 16 | PS_Tray_1474 | D | Area 8 | MD39 | FC5 1-MD3944670 | 19 | FC5_1 | medium drought | 222 | 1790.491437 | 11198.20118 | 9407.709746 | 0.839618568 | -0.04276228 | 0.002743905 | 0.69988539 | 0.677348956 | 0.045435322 | 0.466352042 | 0.693169184 | 15.5490303 | 20.4507 | 3.410641201 | 63.0 | 181.0 | 85.0 | 9.0 | 8.594815825 | 24.69304229 | 11.59618008 | 1.227830832 |
| 3 | 2022-04-19 | 16 | PS_Tray_1474 | D | Area 9 | MD39 | FC5 2-MD3944670 | 19 | FC5_2 | medium drought | 188 | 1666.822338 | 11799.05494 | 10132.23259 | 0.855581044 | -0.053183589 | -0.007837623 | 0.697726846 | 0.678202389 | 0.042456028 | 0.428255193 | 0.673333245 | 16.1709919 | 18.9441 | 2.475699558 | 125.0 | 115.0 | 121.0 | 10.0 | 18.40942563 | 16.93667158 | 17.82032401 | 1.47275405 |
| 4 | 2022-04-19 | 16 | PS_Tray_1474 | D | Area 10 | MD39 | FC4 1-MD3944670 | 19 | FC4_1 | medium drought | 221 | 1705.612675 | 12007.77072 | 10302.15809 | 0.857340532 | 0.134843836 | -0.020678217 | 0.695261926 | 0.683141265 | 0.040467696 | 0.415346996 | 0.651145641 | 17.41491318 | 25.0821 | 2.562847608 | 71.0 | 228.0 | 129.0 | 48.0 | 7.897664071 | 25.36151279 | 14.34927697 | 5.339265851 |
In [ ]:
Copied!
drr = pd.read_csv('/Users/mac/Downloads/drr1_drr2_3rd.csv', sep=';', decimal=',', na_values='#N/A'); drr
drr = pd.read_csv('/Users/mac/Downloads/drr1_drr2_3rd.csv', sep=';', decimal=',', na_values='#N/A'); drr
Out[ ]:
| n | plant_ID | drr1 | drr2 | outlier | |
|---|---|---|---|---|---|
| 0 | 0 | FC5_1_MD5 | 0.497962312 | 0.523980057 | no |
| 1 | 1 | irx14_MD5 | 0.140416022 | 0.102466245 | no |
| 2 | 2 | FC5_1_MD39 | 0.549276448 | 0.630949015 | no |
| 3 | 3 | FC5_2_MD39 | 0.596434441 | 0.525774396 | no |
| 4 | 4 | FC4_1_MD39 | 0.602602133 | 0.753012589 | no |
| ... | ... | ... | ... | ... | ... |
| 692 | 692 | Col0_SD39 | 0.312947394 | 0.299580781 | no |
| 693 | 693 | irx10_C15 | no | ||
| 694 | 694 | FC4_1_C15 | no | ||
| 695 | 695 | Col0_C15 | no | ||
| 696 | 696 | irx9_2_C15 | no |
697 rows × 5 columns
Basic exploration¶
In [3]:
Copied!
df.info()
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 13243 entries, 0 to 13242 Data columns (total 33 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Measuring_date 13243 non-null object 1 Round_Order 13243 non-null int64 2 Tray_ID 13243 non-null object 3 Tray_Info 13243 non-null object 4 Position 13243 non-null object 5 plant_ID_treatment 13243 non-null object 6 plant ID 2 13243 non-null object 7 Day_after_sowing 13243 non-null int64 8 transgenic_line 13243 non-null object 9 treatement 13243 non-null object 10 Size1? 13243 non-null int64 11 Fo 13217 non-null object 12 Fm 13217 non-null object 13 Fv 13217 non-null object 14 QY_max 13217 non-null object 15 NDVI2 11914 non-null object 16 PRI 11914 non-null object 17 SIPI 11914 non-null object 18 NDVI 11914 non-null object 19 PSRI 11914 non-null object 20 MCARI1 11914 non-null object 21 OSAVI 11914 non-null object 22 Size2? 11914 non-null object 23 Area_(mm2) 11757 non-null object 24 Slenderness 11802 non-null object 25 RGB(72,84,58) 12177 non-null float64 26 RGB(73,86,36) 12177 non-null float64 27 RGB(57,71,46) 12177 non-null float64 28 RGB(59,71,20) 12177 non-null float64 29 %RGB(72,84,58) 12177 non-null object 30 %RGB(73,86,36) 12177 non-null object 31 %RGB(57,71,46) 12177 non-null object 32 %RGB(59,71,20) 12177 non-null object dtypes: float64(4), int64(3), object(26) memory usage: 3.3+ MB
Correlation matrix¶
Let's explore the numerics features : ['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI', 'Area_(mm2)', 'Slenderness'] by ploting the correlation matrix
In [4]:
Copied!
columns = ['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI', 'Area_(mm2)', 'Slenderness']
for x in columns:
df[x] = df[x].astype('float')
corr_matrix = df[columns].dropna().corr()
plt.figure(figsize=(15,10))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.show()
columns = ['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI', 'Area_(mm2)', 'Slenderness']
for x in columns:
df[x] = df[x].astype('float')
corr_matrix = df[columns].dropna().corr()
plt.figure(figsize=(15,10))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.show()
Feature engineering¶
In order to prepare our data we've got to write a function for this tasks :
- Considerate only the columns :
['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI', 'Area_(mm2)', 'Slenderness'] - Cast all the numerical columns into float
- Create a joint key
plant_IDin our dataset in order to merge it with the other dataset - Convert the
%RGB(...)columns into 0-1 percentage - Drop the columns
['Size2?','Size1?','RGB(72,84,58)','RGB(73,86,36)','RGB(57,71,46)','RGB(59,71,20)']
In [5]:
Copied!
def convert_percentage_column(df, column_name):
# Remove the '%' sign and convert to float
#df[column_name] = df[column_name].astype(float) / 100.0
df[column_name] = pd.to_numeric(df[column_name], errors='coerce') / 100.0
return df
def feature_eng_basic(df):
#cast all colums to float
columns = ['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI', 'Area_(mm2)', 'Slenderness']
for x in columns:
df[x] = df[x].astype('float')
#add plant_ID column
df['plant_ID'] = df['transgenic_line'] + '_' + df['plant_ID_treatment']
#convert RGB data
convert_percentage_column(df, '%RGB(72,84,58)')
convert_percentage_column(df, '%RGB(73,86,36)')
convert_percentage_column(df, '%RGB(57,71,46)')
convert_percentage_column(df, '%RGB(59,71,20)')
df = df.drop(['Size2?','Size1?','RGB(72,84,58)','RGB(73,86,36)','RGB(57,71,46)','RGB(59,71,20)'],axis=1)
return df
def convert_percentage_column(df, column_name):
# Remove the '%' sign and convert to float
#df[column_name] = df[column_name].astype(float) / 100.0
df[column_name] = pd.to_numeric(df[column_name], errors='coerce') / 100.0
return df
def feature_eng_basic(df):
#cast all colums to float
columns = ['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI', 'Area_(mm2)', 'Slenderness']
for x in columns:
df[x] = df[x].astype('float')
#add plant_ID column
df['plant_ID'] = df['transgenic_line'] + '_' + df['plant_ID_treatment']
#convert RGB data
convert_percentage_column(df, '%RGB(72,84,58)')
convert_percentage_column(df, '%RGB(73,86,36)')
convert_percentage_column(df, '%RGB(57,71,46)')
convert_percentage_column(df, '%RGB(59,71,20)')
df = df.drop(['Size2?','Size1?','RGB(72,84,58)','RGB(73,86,36)','RGB(57,71,46)','RGB(59,71,20)'],axis=1)
return df
In [6]:
Copied!
df = feature_eng_basic(df)
df.info()
df = feature_eng_basic(df)
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 13243 entries, 0 to 13242 Data columns (total 28 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Measuring_date 13243 non-null object 1 Round_Order 13243 non-null int64 2 Tray_ID 13243 non-null object 3 Tray_Info 13243 non-null object 4 Position 13243 non-null object 5 plant_ID_treatment 13243 non-null object 6 plant ID 2 13243 non-null object 7 Day_after_sowing 13243 non-null int64 8 transgenic_line 13243 non-null object 9 treatement 13243 non-null object 10 Fo 13217 non-null float64 11 Fm 13217 non-null float64 12 Fv 13217 non-null float64 13 QY_max 13217 non-null float64 14 NDVI2 11914 non-null float64 15 PRI 11914 non-null float64 16 SIPI 11914 non-null float64 17 NDVI 11914 non-null float64 18 PSRI 11914 non-null float64 19 MCARI1 11914 non-null float64 20 OSAVI 11914 non-null float64 21 Area_(mm2) 11757 non-null float64 22 Slenderness 11802 non-null float64 23 %RGB(72,84,58) 12085 non-null float64 24 %RGB(73,86,36) 12085 non-null float64 25 %RGB(57,71,46) 12085 non-null float64 26 %RGB(59,71,20) 12085 non-null float64 27 plant_ID 13243 non-null object dtypes: float64(17), int64(2), object(9) memory usage: 2.8+ MB
ANOVA quick analysis¶
In [7]:
Copied!
from scipy.stats import f_oneway
#let's focus only on the QY_max parameter for the moment and perform an ANOVA then print the F-statistic and p-value associated across different treatments
data_clean = df.dropna(subset=['QY_max'])
#perform ANOVA for a trait across different treatments
groups = [data_clean['QY_max'][data_clean['treatement'] == treatment] for treatment in data_clean['treatement'].unique()]
f_stat, p_value = f_oneway(*groups)
print(f"ANOVA results for QY_max: F-statistic = {f_stat}, p-value = {p_value}")
from scipy.stats import f_oneway
#let's focus only on the QY_max parameter for the moment and perform an ANOVA then print the F-statistic and p-value associated across different treatments
data_clean = df.dropna(subset=['QY_max'])
#perform ANOVA for a trait across different treatments
groups = [data_clean['QY_max'][data_clean['treatement'] == treatment] for treatment in data_clean['treatement'].unique()]
f_stat, p_value = f_oneway(*groups)
print(f"ANOVA results for QY_max: F-statistic = {f_stat}, p-value = {p_value}")
ANOVA results for QY_max: F-statistic = 333.5911072866381, p-value = 4.5924816064011226e-142
In [10]:
Copied!
#list of features to perform ANOVA on
features = ['QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'MCARI1', 'OSAVI', 'Slenderness']
#dictionary to store p-values
p_values = {}
for feature in features:
groups = [data_clean[feature][data_clean['treatement'] == treatment].dropna() for treatment in data_clean['treatement'].unique()]
_, p_value = f_oneway(*groups)
p_values[feature] = p_value
#convert the dictionary to a DataFrame for visualization
p_values_df = pd.DataFrame(list(p_values.items()), columns=['Feature', 'p-value']).set_index('Feature')
#visualize p-values using a heatmap
plt.figure(figsize=(10, 8))
sns.heatmap(p_values_df, annot=True, cmap='coolwarm_r', cbar_kws={'label': 'p-value'})
plt.title('p-values from ANOVA across treatments')
plt.show()
#list of features to perform ANOVA on
features = ['QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'MCARI1', 'OSAVI', 'Slenderness']
#dictionary to store p-values
p_values = {}
for feature in features:
groups = [data_clean[feature][data_clean['treatement'] == treatment].dropna() for treatment in data_clean['treatement'].unique()]
_, p_value = f_oneway(*groups)
p_values[feature] = p_value
#convert the dictionary to a DataFrame for visualization
p_values_df = pd.DataFrame(list(p_values.items()), columns=['Feature', 'p-value']).set_index('Feature')
#visualize p-values using a heatmap
plt.figure(figsize=(10, 8))
sns.heatmap(p_values_df, annot=True, cmap='coolwarm_r', cbar_kws={'label': 'p-value'})
plt.title('p-values from ANOVA across treatments')
plt.show()
The p-values of these parameters are very low, that's generally a good sign in statistics 🤓
Merge datasets and compute features ratio¶
We not only want to merge our two datasets but computing the parameters ratio. We call parameters ratio the value of the parameter for a given time period divide by the average value of it's trangenic_line sibiling for the control treatement.
For example the parameter NDVI for the day 22 will be called ratio_NDVI on the day=22. The ratio_NDVI is the division of the given row (for example FC5_2) by the average value of the same transgenic_line==FC5_2 for the treatement==control as you can see below in the compute_ratios_and_merge() function.
Then we will split the dataset by treatement in two parts :
- SD : severe drought treatement
- MD : medium drought treatement
In [13]:
Copied!
def compute_ratios_and_merge(df_main, df_other_path, day, stat="mean"):
"""
Compute ratios for specified columns based on a given day and statistical measure,
and merge with another dataframe.
Parameters:
- df_main (pd.DataFrame): The main input dataframe.
- df_other_path (str): Path to the other dataframe to be merged with the main dataframe.
- day (int): The day after sowing to consider for the visualization.
- stat (str): The statistical measure to compute. Default is "mean".
Currently, only "mean" is supported.
Returns:
- tuple: Two dataframes (sd, md) filtered by 'plant ID 2' containing 'SD' and 'MD' respectively.
"""
# Load the other dataframe
df_other = pd.read_csv(df_other_path, sep=';', decimal=',', na_values='#N/A')
df_other = df_other[(df_other['drr1'].str.strip() != '') & (df_other['drr2'].str.strip() != '')]
# Columns to consider for ratio computation
columns_to_consider = ['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI','Slenderness']
# Filter dataframe for 'treatement' == 'control' and the specified day
control_df = df_main[(df_main['treatement'] == 'control') & (df_main['Day_after_sowing'] == day)]
# Check the statistical measure and compute accordingly
if stat == "mean":
# Compute mean for the specified columns grouped by 'transgenic_line'
mean_df = control_df.groupby(['transgenic_line'])[columns_to_consider].mean().reset_index()
else:
raise ValueError(f"Unsupported statistical measure: {stat}")
# Rename columns in mean_df for merging
mean_df = mean_df.rename(columns={col: f"mean_{col}" for col in columns_to_consider})
# Merge the original dataframe with mean_df
merged_df_main = df_main.merge(mean_df, on=['transgenic_line'], how='left')
# Compute the ratio for each specified column
for col in columns_to_consider:
merged_df_main[f"ratio_{col}"] = merged_df_main[col] / merged_df_main[f"mean_{col}"]
# Create a new column in the main dataframe to match the format of plant_ID in the second dataframe
merged_df_main['plant_ID'] = merged_df_main['transgenic_line'] + '_' + merged_df_main['plant_ID_treatment']
# Merge the two dataframes on the plant_ID column
final_merged_df = pd.merge(merged_df_main, df_other, on='plant_ID', how='inner')
# Filter the merged dataframe based on the specified day
filtre = final_merged_df[final_merged_df['Day_after_sowing'] == day]
md = filtre[filtre['plant ID 2'].str.contains('MD')]
sd = filtre[filtre['plant ID 2'].str.contains('SD')]
return sd, md
def compute_ratios_and_merge(df_main, df_other_path, day, stat="mean"):
"""
Compute ratios for specified columns based on a given day and statistical measure,
and merge with another dataframe.
Parameters:
- df_main (pd.DataFrame): The main input dataframe.
- df_other_path (str): Path to the other dataframe to be merged with the main dataframe.
- day (int): The day after sowing to consider for the visualization.
- stat (str): The statistical measure to compute. Default is "mean".
Currently, only "mean" is supported.
Returns:
- tuple: Two dataframes (sd, md) filtered by 'plant ID 2' containing 'SD' and 'MD' respectively.
"""
# Load the other dataframe
df_other = pd.read_csv(df_other_path, sep=';', decimal=',', na_values='#N/A')
df_other = df_other[(df_other['drr1'].str.strip() != '') & (df_other['drr2'].str.strip() != '')]
# Columns to consider for ratio computation
columns_to_consider = ['Fo', 'Fm', 'Fv', 'QY_max', 'NDVI2', 'PRI', 'SIPI', 'NDVI', 'PSRI', 'MCARI1', 'OSAVI','Slenderness']
# Filter dataframe for 'treatement' == 'control' and the specified day
control_df = df_main[(df_main['treatement'] == 'control') & (df_main['Day_after_sowing'] == day)]
# Check the statistical measure and compute accordingly
if stat == "mean":
# Compute mean for the specified columns grouped by 'transgenic_line'
mean_df = control_df.groupby(['transgenic_line'])[columns_to_consider].mean().reset_index()
else:
raise ValueError(f"Unsupported statistical measure: {stat}")
# Rename columns in mean_df for merging
mean_df = mean_df.rename(columns={col: f"mean_{col}" for col in columns_to_consider})
# Merge the original dataframe with mean_df
merged_df_main = df_main.merge(mean_df, on=['transgenic_line'], how='left')
# Compute the ratio for each specified column
for col in columns_to_consider:
merged_df_main[f"ratio_{col}"] = merged_df_main[col] / merged_df_main[f"mean_{col}"]
# Create a new column in the main dataframe to match the format of plant_ID in the second dataframe
merged_df_main['plant_ID'] = merged_df_main['transgenic_line'] + '_' + merged_df_main['plant_ID_treatment']
# Merge the two dataframes on the plant_ID column
final_merged_df = pd.merge(merged_df_main, df_other, on='plant_ID', how='inner')
# Filter the merged dataframe based on the specified day
filtre = final_merged_df[final_merged_df['Day_after_sowing'] == day]
md = filtre[filtre['plant ID 2'].str.contains('MD')]
sd = filtre[filtre['plant ID 2'].str.contains('SD')]
return sd, md
In [16]:
Copied!
day=22
sd, md = compute_ratios_and_merge(df, '/Users/mac/Downloads/drr_22_to_37.csv', day=day)
sd.head()
day=22
sd, md = compute_ratios_and_merge(df, '/Users/mac/Downloads/drr_22_to_37.csv', day=day)
sd.head()
Out[16]:
| Measuring_date | Round_Order | Tray_ID | Tray_Info | Position | plant_ID_treatment | plant ID 2 | Day_after_sowing | transgenic_line | treatement | Fo | Fm | Fv | QY_max | NDVI2 | PRI | SIPI | NDVI | PSRI | MCARI1 | OSAVI | Area_(mm2) | Slenderness | %RGB(72,84,58) | %RGB(73,86,36) | %RGB(57,71,46) | %RGB(59,71,20) | plant_ID | mean_Fo | mean_Fm | mean_Fv | mean_QY_max | mean_NDVI2 | mean_PRI | mean_SIPI | mean_NDVI | mean_PSRI | mean_MCARI1 | mean_OSAVI | mean_Slenderness | ratio_Fo | ratio_Fm | ratio_Fv | ratio_QY_max | ratio_NDVI2 | ratio_PRI | ratio_SIPI | ratio_NDVI | ratio_PSRI | ratio_MCARI1 | ratio_OSAVI | ratio_Slenderness | n | outlier | drr1 | drr2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 136 | 2022-04-22 | 22 | PS_Tray_1418 | C | Area 5 | SD3 | FC5 2-SD344673 | 22 | FC5_2 | severe drought | 1938.118361 | 13385.70647 | 11447.58809 | 0.856718 | 0.164980 | -0.024997 | 0.733035 | 0.724730 | 0.041247 | 0.535999 | 0.738571 | 47.1789 | 3.784743 | 0.132466 | 0.284447 | 0.117682 | 0.028977 | FC5_2_SD3 | 2095.653840 | 13474.071738 | 11378.417903 | 0.842635 | 0.064934 | -0.002228 | 0.729190 | 0.728549 | 0.027970 | 0.518484 | 0.717085 | 7.903370 | 0.924828 | 0.993442 | 1.006079 | 1.016713 | 2.540748 | 11.220782 | 1.005273 | 0.994758 | 1.474668 | 1.033781 | 1.029963 | 0.478877 | 7 | no | 0.271889852 | 0.468326358 |
| 155 | 2022-04-22 | 22 | PS_Tray_1418 | C | Area 9 | SD3 | FC5 1-SD344673 | 22 | FC5_1 | severe drought | 2023.216741 | 13710.18928 | 11686.97255 | 0.853230 | -0.042872 | -0.007269 | 0.716099 | 0.698858 | 0.043679 | 0.564413 | 0.752266 | 44.0262 | 3.757288 | 0.089987 | 0.150824 | 0.115970 | 0.006971 | FC5_1_SD3 | 2078.022108 | 13377.230331 | 11299.208221 | 0.843251 | 0.053044 | -0.004348 | 0.725985 | 0.722155 | 0.029840 | 0.514453 | 0.712399 | 6.676540 | 0.973626 | 1.024890 | 1.034318 | 1.011835 | -0.808243 | 1.671831 | 0.986382 | 0.967740 | 1.463750 | 1.097113 | 1.055962 | 0.562760 | 8 | no | 0.063879637 | 0.25875854 |
| 174 | 2022-04-22 | 22 | PS_Tray_1418 | C | Area 11 | SD3 | FC4 1-SD344673 | 22 | FC4_1 | severe drought | 1947.707120 | 12900.15193 | 10952.44482 | 0.850966 | 0.154246 | -0.006981 | 0.708555 | 0.698321 | 0.045711 | 0.484275 | 0.712234 | 35.5725 | 4.894902 | 0.105098 | 0.199216 | 0.130196 | 0.021176 | FC4_1_SD3 | 2046.423985 | 13040.031125 | 10993.607141 | 0.841225 | 0.055439 | -0.005959 | 0.717233 | 0.710647 | 0.033785 | 0.489776 | 0.697524 | 7.053135 | 0.951761 | 0.989273 | 0.996256 | 1.011580 | 2.782272 | 1.171490 | 0.987902 | 0.982656 | 1.352985 | 0.988769 | 1.021090 | 0.694004 | 9 | no | 0.148904801 | 0.067751532 |
| 193 | 2022-04-22 | 22 | PS_Tray_1418 | C | Area 12 | SD3 | FC4 2-SD344673 | 22 | FC4_2 | severe drought | 2175.084019 | 13803.20649 | 11628.12247 | 0.839968 | 0.125841 | 0.005419 | 0.719040 | 0.719307 | 0.031061 | 0.518520 | 0.715514 | 68.0760 | 7.804918 | 0.056967 | 0.234016 | 0.079918 | 0.048770 | FC4_2_SD3 | 2140.238333 | 13637.798401 | 11497.560065 | 0.840809 | 0.070690 | -0.002861 | 0.732657 | 0.729802 | 0.031429 | 0.518463 | 0.715397 | 8.846905 | 1.016281 | 1.012129 | 1.011356 | 0.999000 | 1.780186 | -1.894273 | 0.981415 | 0.985619 | 0.988273 | 1.000110 | 1.000163 | 0.882220 | 10 | yes | 0.27785895 | -0.446619999 |
| 212 | 2022-04-22 | 22 | PS_Tray_1418 | C | Area 13 | SD3 | irx10-SD344673 | 22 | irx10 | severe drought | 2475.800994 | 14271.94008 | 11796.13907 | 0.826229 | 0.102867 | 0.003251 | 0.724768 | 0.717923 | 0.042136 | 0.527126 | 0.724767 | 62.7192 | 5.480872 | 0.063167 | 0.260231 | 0.089858 | 0.039591 | irx10_SD3 | 2151.480402 | 13128.398512 | 10976.918116 | 0.833489 | 0.059166 | -0.007578 | 0.725290 | 0.716681 | 0.036171 | 0.507240 | 0.710071 | 7.415835 | 1.150743 | 1.087104 | 1.074631 | 0.991290 | 1.738635 | -0.429000 | 0.999281 | 1.001733 | 1.164917 | 1.039203 | 1.020696 | 0.739077 | 11 | yes | 0.093561833 | 0.14657061 |
In [17]:
Copied!
md.head()
md.head()
Out[17]:
| Measuring_date | Round_Order | Tray_ID | Tray_Info | Position | plant_ID_treatment | plant ID 2 | Day_after_sowing | transgenic_line | treatement | Fo | Fm | Fv | QY_max | NDVI2 | PRI | SIPI | NDVI | PSRI | MCARI1 | OSAVI | Area_(mm2) | Slenderness | %RGB(72,84,58) | %RGB(73,86,36) | %RGB(57,71,46) | %RGB(59,71,20) | plant_ID | mean_Fo | mean_Fm | mean_Fv | mean_QY_max | mean_NDVI2 | mean_PRI | mean_SIPI | mean_NDVI | mean_PSRI | mean_MCARI1 | mean_OSAVI | mean_Slenderness | ratio_Fo | ratio_Fm | ratio_Fv | ratio_QY_max | ratio_NDVI2 | ratio_PRI | ratio_SIPI | ratio_NDVI | ratio_PSRI | ratio_MCARI1 | ratio_OSAVI | ratio_Slenderness | n | outlier | drr1 | drr2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 2022-04-22 | 22 | PS_Tray_1400 | E | Area 7 | MD5 | FC5 1-MD544673 | 22 | FC5_1 | medium drought | 1902.768960 | 11990.128350 | 10087.359390 | 0.839354 | 0.142469 | -0.005962 | 0.698264 | 0.689344 | 0.046073 | 0.482799 | 0.704452 | 34.4844 | 7.456311 | 0.039644 | 0.245146 | 0.101133 | 0.031553 | FC5_1_MD5 | 2078.022108 | 13377.230331 | 11299.208221 | 0.843251 | 0.053044 | -0.004348 | 0.725985 | 0.722155 | 0.029840 | 0.514453 | 0.712399 | 6.676540 | 0.915663 | 0.896309 | 0.892749 | 0.995379 | 2.685882 | 1.371324 | 0.961816 | 0.954566 | 1.543997 | 0.938471 | 0.988845 | 1.116793 | 0 | no | 0.497962312 | 0.608625678 |
| 22 | 2022-04-22 | 22 | PS_Tray_1400 | E | Area 19 | MD5 | irx14-MD544673 | 22 | irx14 | medium drought | 1050.925528 | 8894.538974 | 7843.613515 | 0.877019 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 5.8311 | 1.550239 | 0.191388 | 0.287081 | 0.162679 | 0.023923 | irx14_MD5 | 1990.468331 | 12749.856962 | 10759.388630 | 0.840149 | 0.016619 | -0.009124 | 0.713908 | 0.703522 | 0.039245 | 0.478745 | 0.696220 | 5.591186 | 0.527979 | 0.697619 | 0.729002 | 1.043885 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.277265 | 1 | no | 0.142991914 | 0.140897002 |
| 41 | 2022-04-22 | 22 | PS_Tray_1474 | D | Area 8 | MD39 | FC5 1-MD3944673 | 22 | FC5_1 | medium drought | 2190.587033 | 13693.086460 | 11502.499440 | 0.839254 | 0.025056 | -0.009800 | 0.705407 | 0.675368 | 0.063946 | 0.546744 | 0.745734 | 46.3698 | 12.476534 | 0.041516 | 0.225632 | 0.105295 | 0.018051 | FC5_1_MD39 | 2078.022108 | 13377.230331 | 11299.208221 | 0.843251 | 0.053044 | -0.004348 | 0.725985 | 0.722155 | 0.029840 | 0.514453 | 0.712399 | 6.676540 | 1.054169 | 1.023611 | 1.017992 | 0.995260 | 0.472369 | 2.253910 | 0.971655 | 0.935213 | 2.142933 | 1.062769 | 1.046793 | 1.868713 | 2 | no | 0.549276448 | 0.752359451 |
| 60 | 2022-04-22 | 22 | PS_Tray_1474 | D | Area 9 | MD39 | FC5 2-MD3944673 | 22 | FC5_2 | medium drought | 2076.428258 | 14051.999070 | 11975.570780 | 0.849392 | 0.020800 | -0.006022 | 0.725753 | 0.707791 | 0.048438 | 0.572262 | 0.755250 | 37.5813 | 3.742390 | 0.092799 | 0.224944 | 0.116555 | 0.015590 | FC5_2_MD39 | 2095.653840 | 13474.071738 | 11378.417903 | 0.842635 | 0.064934 | -0.002228 | 0.729190 | 0.728549 | 0.027970 | 0.518484 | 0.717085 | 7.903370 | 0.990826 | 1.042892 | 1.052481 | 1.008019 | 0.320330 | 2.702998 | 0.995287 | 0.971509 | 1.731786 | 1.103720 | 1.053224 | 0.473518 | 3 | no | 0.596434441 | 0.63499381 |
| 79 | 2022-04-22 | 22 | PS_Tray_1474 | D | Area 10 | MD39 | FC4 1-MD3944673 | 22 | FC4_1 | medium drought | 1991.953173 | 13304.655360 | 11312.702200 | 0.850039 | 0.210979 | -0.029469 | 0.718386 | 0.707784 | 0.047684 | 0.493320 | 0.711991 | 49.8294 | 5.825308 | 0.054871 | 0.250280 | 0.109742 | 0.031915 | FC4_1_MD39 | 2046.423985 | 13040.031125 | 10993.607141 | 0.841225 | 0.055439 | -0.005959 | 0.717233 | 0.710647 | 0.033785 | 0.489776 | 0.697524 | 7.053135 | 0.973382 | 1.020293 | 1.029026 | 1.010478 | 3.805615 | 4.945214 | 1.001609 | 0.995972 | 1.411385 | 1.007237 | 1.020740 | 0.825917 | 4 | no | 0.602602133 | 0.812206262 |
Plot the heatmap Dendrogram¶
Let's see how we can form a heatmap Dendrogram with few features : ['%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr1', 'drr2']
In [19]:
Copied!
from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn.preprocessing import StandardScaler
import numpy as np
def plot_heatmap_with_dendrogram(df):
# Features to consider
features = ['%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr1', 'drr2']
# Convert drr1 and drr2 columns to float
df['drr1'] = df['drr1'].astype(float)
df['drr2'] = df['drr2'].astype(float)
# Group by 'transgenic_line' and compute the mean for each feature
grouped_data = df.groupby('transgenic_line')[features].mean()
# Normalize the data
scaler = StandardScaler()
data_normalized = scaler.fit_transform(grouped_data)
# Check for non-finite values
if not np.all(np.isfinite(data_normalized)):
print("Warning: Non-finite values detected in the normalized data.")
return
# Compute the linkage matrix for hierarchical clustering
row_linkage = linkage(data_normalized, method='average')
# Plot the heatmap with dendrogram
sns.clustermap(grouped_data, row_linkage=row_linkage, col_cluster=False, figsize=(10, 8), cmap='viridis')
plt.show()
# Call the function
plot_heatmap_with_dendrogram(sd)
from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn.preprocessing import StandardScaler
import numpy as np
def plot_heatmap_with_dendrogram(df):
# Features to consider
features = ['%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr1', 'drr2']
# Convert drr1 and drr2 columns to float
df['drr1'] = df['drr1'].astype(float)
df['drr2'] = df['drr2'].astype(float)
# Group by 'transgenic_line' and compute the mean for each feature
grouped_data = df.groupby('transgenic_line')[features].mean()
# Normalize the data
scaler = StandardScaler()
data_normalized = scaler.fit_transform(grouped_data)
# Check for non-finite values
if not np.all(np.isfinite(data_normalized)):
print("Warning: Non-finite values detected in the normalized data.")
return
# Compute the linkage matrix for hierarchical clustering
row_linkage = linkage(data_normalized, method='average')
# Plot the heatmap with dendrogram
sns.clustermap(grouped_data, row_linkage=row_linkage, col_cluster=False, figsize=(10, 8), cmap='viridis')
plt.show()
# Call the function
plot_heatmap_with_dendrogram(sd)
This is not bad, but we do not have exploited all the informations on this type of graph. We want to add an other dimension in order to have 2 dendrograms on the two axis of our graph and print the numeric values because I am not a fan of only-colours graph 🤓
Plot 2D Dendrogram¶
In [20]:
Copied!
def plot_heatmap_with_dendrogram_2d_ratio(df,typo,day, features=['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr1', 'drr2']):
"""
Plots a heatmap with dendrogram for the given dataframe based on specified features.
This function takes a dataframe, processes it by grouping on the 'transgenic_line' column,
and computes the mean for each feature. It then scales the features and plots a heatmap
with dendrograms for both rows and columns. The heatmap is saved as a PNG file.
Parameters:
- df (pd.DataFrame): The input dataframe containing the data to be plotted.
- typo (str): The name used for the title and filename of the plot.
- day (int): The day for which the data is considered, used for the title and filename of the plot.
- features (list of str, optional): List of features/columns to consider from the dataframe.
Defaults to a predefined list of features.
Returns:
- None: The function saves the heatmap as a PNG file and displays it, but does not return any value.
Warnings:
- If non-finite values are detected in the normalized data, a warning message is printed.
Dependencies:
- Requires seaborn (as sns), matplotlib.pyplot (as plt), numpy (as np), and
sklearn.preprocessing.StandardScaler for execution.
Example:
>>> day = 22
>>> sd, md = compute_ratios_and_merge(df, '/path/to/file.csv', time_window={"22": [day]}, day=day)
>>> plot_heatmap_with_dendrogram_2d_ratio(md, 'medium drought', day, ['ratio_Slenderness', ...])
"""
# Features to consider
if not features:
features = ['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr1', 'drr2']
to_scale = ['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI']
# Convert drr1 and drr2 columns to float
df['drr1'] = df['drr1'].astype(float)
df['drr2'] = df['drr2'].astype(float)
# Group by 'transgenic_line' and compute the mean for each feature
grouped_data = df.groupby('transgenic_line')[features].mean()
# Features to scale
to_scale = features
# Scale the specified features
scaler = StandardScaler()
grouped_data[to_scale] = scaler.fit_transform(grouped_data[to_scale])
# Check for non-finite values
if not np.all(np.isfinite(grouped_data)):
print("Warning: Non-finite values detected in the normalized data.")
return
# Compute the linkage matrix for hierarchical clustering
row_linkage = linkage(grouped_data, method='average')
col_linkage = linkage(grouped_data.T, method='average') # Transpose for column clustering
# Plot the heatmap with dendrogram
g = sns.clustermap(grouped_data, row_linkage=row_linkage, col_linkage=col_linkage, figsize=(18, 12), cmap='viridis',annot=True, fmt=".2f")
plt.title(f"Heatmap Dendrogram for {typo} | day={day}")
plt.show()
#g.savefig(f"Heatmap Dendrogram for {typo} day={day}.png")
def plot_heatmap_with_dendrogram_2d_ratio(df,typo,day, features=['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr1', 'drr2']):
"""
Plots a heatmap with dendrogram for the given dataframe based on specified features.
This function takes a dataframe, processes it by grouping on the 'transgenic_line' column,
and computes the mean for each feature. It then scales the features and plots a heatmap
with dendrograms for both rows and columns. The heatmap is saved as a PNG file.
Parameters:
- df (pd.DataFrame): The input dataframe containing the data to be plotted.
- typo (str): The name used for the title and filename of the plot.
- day (int): The day for which the data is considered, used for the title and filename of the plot.
- features (list of str, optional): List of features/columns to consider from the dataframe.
Defaults to a predefined list of features.
Returns:
- None: The function saves the heatmap as a PNG file and displays it, but does not return any value.
Warnings:
- If non-finite values are detected in the normalized data, a warning message is printed.
Dependencies:
- Requires seaborn (as sns), matplotlib.pyplot (as plt), numpy (as np), and
sklearn.preprocessing.StandardScaler for execution.
Example:
>>> day = 22
>>> sd, md = compute_ratios_and_merge(df, '/path/to/file.csv', time_window={"22": [day]}, day=day)
>>> plot_heatmap_with_dendrogram_2d_ratio(md, 'medium drought', day, ['ratio_Slenderness', ...])
"""
# Features to consider
if not features:
features = ['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr1', 'drr2']
to_scale = ['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI']
# Convert drr1 and drr2 columns to float
df['drr1'] = df['drr1'].astype(float)
df['drr2'] = df['drr2'].astype(float)
# Group by 'transgenic_line' and compute the mean for each feature
grouped_data = df.groupby('transgenic_line')[features].mean()
# Features to scale
to_scale = features
# Scale the specified features
scaler = StandardScaler()
grouped_data[to_scale] = scaler.fit_transform(grouped_data[to_scale])
# Check for non-finite values
if not np.all(np.isfinite(grouped_data)):
print("Warning: Non-finite values detected in the normalized data.")
return
# Compute the linkage matrix for hierarchical clustering
row_linkage = linkage(grouped_data, method='average')
col_linkage = linkage(grouped_data.T, method='average') # Transpose for column clustering
# Plot the heatmap with dendrogram
g = sns.clustermap(grouped_data, row_linkage=row_linkage, col_linkage=col_linkage, figsize=(18, 12), cmap='viridis',annot=True, fmt=".2f")
plt.title(f"Heatmap Dendrogram for {typo} | day={day}")
plt.show()
#g.savefig(f"Heatmap Dendrogram for {typo} day={day}.png")
In [21]:
Copied!
plot_heatmap_with_dendrogram_2d_ratio(sd,'severe drought',day,['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr2'])
plot_heatmap_with_dendrogram_2d_ratio(sd,'severe drought',day,['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr2'])
In [22]:
Copied!
plot_heatmap_with_dendrogram_2d_ratio(md,'medium drought',day,['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr2'])
plot_heatmap_with_dendrogram_2d_ratio(md,'medium drought',day,['ratio_Slenderness','ratio_Fo', 'ratio_Fm', 'ratio_QY_max', 'ratio_NDVI2', 'ratio_PRI',
'ratio_NDVI', 'ratio_PSRI', 'ratio_OSAVI','%RGB(72,84,58)', '%RGB(73,86,36)', '%RGB(57,71,46)', '%RGB(59,71,20)', 'drr2'])
Conclusion¶
In this article we have seen how to understand a Hierarchical clustering and how to apply this in bio-informatic.
Many people like Hierarchical approach because we do not need to specify number of clusters in advance unlike k-means and of course for the Dendrogram visualization who provides a deep insight into the hierarchical structure of data.
Flexibility with Distance Metrics: Can work with any distance metric (Euclidean, Manhattan, etc.). Can Handle Non-Spherical Data: Especially with linkage methods like single linkage. Be carful, Hierarchical methods can be computationally intensive especially for larger datasets, the algorithm can be very slow and sensitive to noise, Single linkage, in particular, is sensitive to noise and outliers.
Be aware of the fixed Linkage Criteria also. The choice of linkage criteria can significantly affect the results, and there's no one-size-fits-all.