Classification and Regression Trees (CART)¶
Overview¶
This course aims to make you understand the theoretical principles of decision trees and to make you code a simple example of application.
Decision trees are part of the field of recursive partitioning methods, which are better known by the acronym CART (Classification And Regression Tree) which make it possible to establish successive rules making it possible to classify observations or to make regressions. .
We speak of classification when the target variable is qualitative (categorical), a case that we will deal with later. In this introduction we are interested in the Regression Trees which intervene in the case of a quantitative target variable. Their advantage lies in particular in their easily readable graphical representation, which makes them good choices for modeling business issues.
A tree is made up of three types of elements:
- The root, where all the training data resides.
- The nodes/branches, which represents the points from the root where the data are separated into two groups according to a criterion linked to the explanatory variables.
- The leaves, which are the terminal nodes of the tree and to which are associated a value in the case where Y is quantitative and a class when Y is qualitative.
Thus, from the root, a node is defined which divides all the data according to a criterion linked to an explanatory variable, for each of the two branches thus created, the same process is repeated, and so on until no division does not satisfy the construction criterion of a node and a terminal or leaf node is then defined.
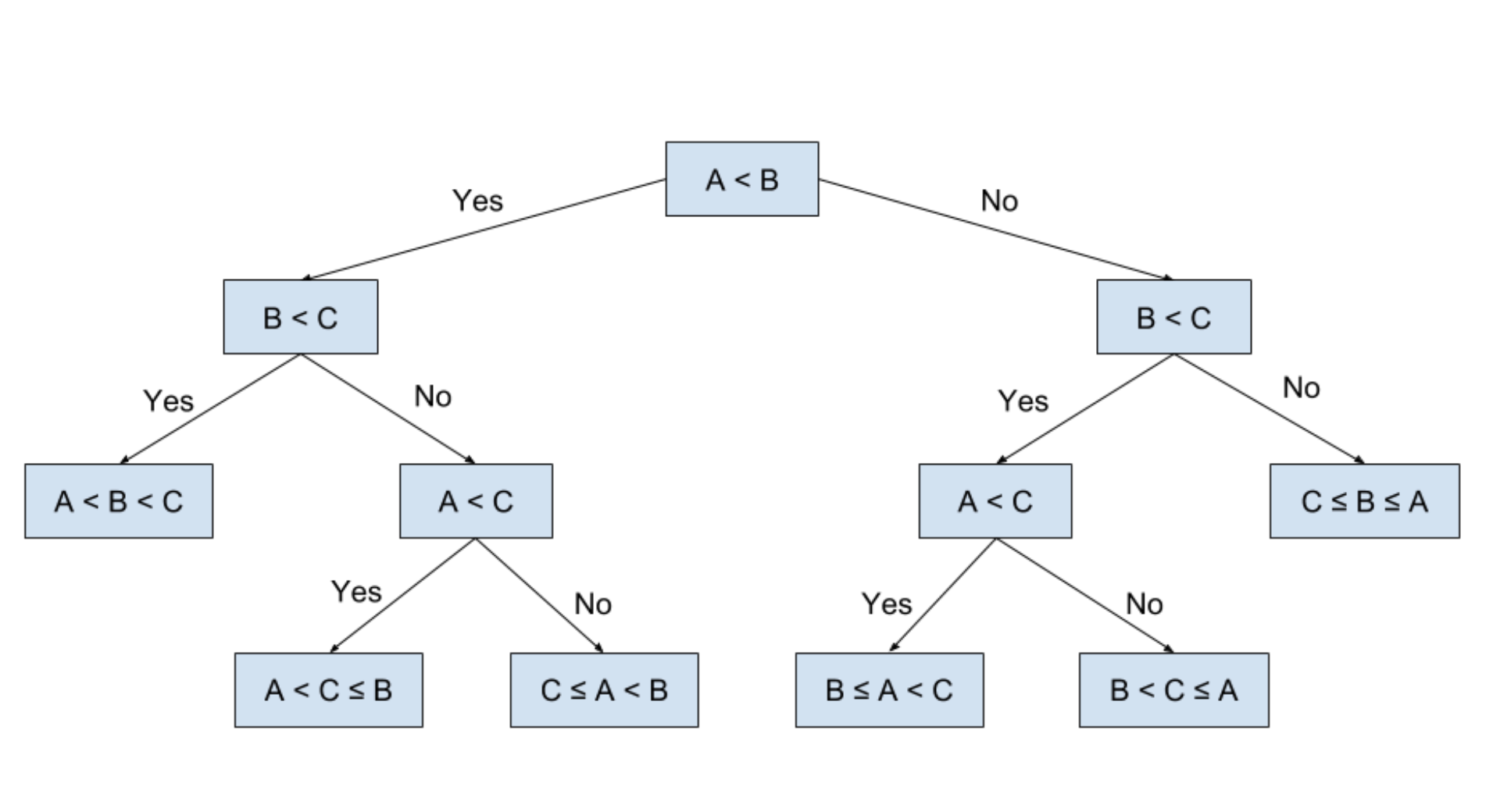
Here is an example of a tree with the root at the top and the first division and the sequence of the branches, up to the leaves. In addition, one immediately notices the very clear and visual aspect of the tree. Let's imagine that we have a program that requests three values from a user and that aims to classify these three values. To answer the problem we use a decision tree like the one above.
Let's see how to read this tree representation, for that you have to start by looking at the node at the very top and check if the condition applies. As indicated in the diagram, if so we go to the left towards the lower node to check (or not) the new condition. And this until there is no lower node.
To do this algorithm needs several things:
- A criterion for selecting the best division
- A rule to define if a node is terminal
- A method to assign each sheet a value or a class
The mathematical notation of the problem: the division criterion¶
As stated in the previous part, in order to build a decision tree, we need a criterion for selecting the best division for a node.
A node is eligible if the resulting branches carry non-empty nodes (i.e. at least one observation belongs to each of the child nodes). For a parent node containing M observations there are M - 1 admissible divisions if the variable selected for the division is quantitative or qualitative ordinal, and admissible divisions if the selected variable is nominal.
In order to select the best admissible division, we construct a heterogeneity function which has two remarkable properties:
- It is zero when all the individuals belong to the same modality or have the same value of Y.
- It is maximum when the values of Y are evenly distributed in the node.
We therefore seek the division which minimizes the sum of the heterogeneities of the child nodes.
The mathematical notation of the problem: the stopping criterion¶
A given node will be terminal when it is homogeneous, that is to say that all the observations in the node present the same value or the same modality of Y, when there are no more admissible divisions, or when the number observations in the node is lower than a value defined in advance, in general of the order of a few units.
If Y is a quantitative variable In the case of regression, the heterogeneity of node k is written as follows:
$$H_k=\frac{1}{Card(k)}\cdot\sum_{i\in{k}}(y_i-\bar{y_k})^2$$
$Card(k)$ sometimes also denoted #(k) or $|k|$ is the number of elements in the node $k$, and $\bar{y}_k$ is the average of the values of $Y$ among the observations of the node $k$. What makes the variance of the node $k$. The division retained is that for which: $H_{kG}+H_{kD}$ the sum of the heterogeneity of the left branch and the right branch is minimal. Because let us recall the the objective is to divide the individuals into two groups that are the most homogeneous with respect to our target variable. This may seem complex but you will see the python tools make our task much easier.
If Y is a qualitative variable Let Y be a qualitative variable with m modalities or categories numbered from 1 to m. The preferred heterogeneity function most of the time is the concentration of GINI which is noted as follows:
$$H_k=\sum_{i=1}^{m}p_{k}^{i}\cdot(1-p_{k}^{i})$$
Where $p^i_k$ is the proportion of individuals of class $i$ of $Y$ in node $k$.
As before, for each node it is a question of finding, among the admissible divisions, the one that maximizes the decrease in heterogeneity.
Pruning a tree¶
The problem with regression models like LASSO and RIDGE is that there is a risk, as with any supervised learning problem, of over-learning.
As a reminder, overfitting means that your algorithm is so trained on your data that it loses its ability to generalize its predictions. The stopping criterion defined for the construction of the tree is often conducive to over-fitting since it is very likely that most of the leaves of the tree contain only a few observations, we will illustrate this example later.
Thus the decision tree as it is will be very unstable, its bias is almost zero or even zero by definition, it depends very strongly on the observations of the learning base and will potentially not be generalizable to new data.
Our problem is therefore to find an intermediate tree that satisfies an interesting bias-variance compromise for the purposes of estimating $Y$. This is why we are going to see the random drills (in sets of trees) which will precisely respond to this problem. We will see random drills in the next part, don't panic.
Le critere de GINI¶
The Gini index, also known as the Gini coefficient or Gini impurity, is a measure of inequality or impurity in a dataset. In the context of decision trees, it's used to quantify the impurity of a node, which in turn helps us determine the best feature to split the dataset on.
The Gini index ranges between 0 and 1, with 0 representing perfect purity (all instances in a node belong to a single class) and 1 representing maximum impurity (instances are distributed uniformly across all classes).
The CART algorithm can uses the Gini index to choose the best split at each node of the tree. The algorithm calculates the Gini index for each potential split and selects the split that results in the lowest weighted Gini index.
Exemple de code gini_index function¶
Now let's dive into some Python examples to illustrate these concepts. First, we'll start with a simple function to calculate the Gini index of a dataset:
def gini_index(groups, classes):
total_instances = sum([len(group) for group in groups])
gini = 0.0
for group in groups:
group_size = len(group)
if group_size == 0:
continue
score = 0.0
for class_val in classes:
proportion = [row[-1] for row in group].count(class_val) / group_size
score += proportion * proportion
gini += (1 - score) * (group_size / total_instances)
return gini
#Now let's consider a toy dataset with two features and a binary class label (A,B)
dataset = [
[1, 1, 'A'],
[1, 2, 'A'],
[2, 1, 'B'],
[2, 2, 'B'],
[3, 1, 'A'],
[3, 2, 'A'],
[4, 1, 'B'],
[4, 2, 'B'],
]
We can now use our gini_index() function to evaluate the Gini index for different splits:
# Example splits:
# Split 1: [1, 1, 'A'], [1, 2, 'A'] | [2, 1, 'B'], [2, 2, 'B'], [3, 1, 'A'], [3, 2, 'A'], [4, 1, 'B'], [4, 2, 'B']
# Split 2: [1, 1, 'A'], [1, 2, 'A'], [2, 1, 'B'], [2, 2, 'B'] | [3, 1, 'A'], [3, 2, 'A'], [4, 1, 'B'], [4, 2, 'B']
split1 = (dataset[:2], dataset[2:])
split2 = (dataset[:4], dataset[4:])
classes = list(set(row[-1] for row in dataset))
print("Gini index for split 1:", gini_index(split1, classes))
print("Gini index for split 2:", gini_index(split2, classes))
Gini index for split 1: 0.3333333333333333 Gini index for split 2: 0.5
In this case, the second split results in a Gini index of 0, which means it perfectly separates the classes. The CART algorithm would choose the minimal possible value for a split.
Other CART split metrics for classification¶
In addition to the Gini index, there are other metrics used for splitting nodes in decision trees. Two popular alternatives are Information Gain and Gain Ratio. Let's discuss each of them.
Information Gain¶
Information Gain is based on the concept of entropy, which measures the impurity of an input set. In the context of decision trees, it measures the reduction in entropy achieved by partitioning a dataset based on a particular feature. The attribute with the highest Information Gain is selected as the splitting attribute.
Entropy is calculated using the following formula:
$$ Entropy(S) = -Σ P(c) * log2(P(c))$$
Where S is the dataset, c represents a class, and P(c) is the proportion of instances belonging to class c.
Information Gain is calculated as:
$$ InformationGain(S, A) = Entropy(S) - Σ (|Sv| / |S|) * Entropy(Sv) $$
Where S is the dataset, A is the attribute we are considering, Sv is the subset of S where the attribute A has value v, and $|Sv| / |S|$ is the proportion of instances in Sv.
Gain Ratio¶
The Gain Ratio is an extension of Information Gain that takes into account the intrinsic information of an attribute. It is useful in dealing with the bias of Information Gain towards attributes with more distinct values.
Gain Ratio is calculated as:
$$ GainRatio(S, A) = InformationGain(S, A) / SplitInformation(S, A) $$
Where SplitInformation(S, A) is the entropy of the attribute A.
Now, let's discuss the differences between Gini and other metrics:
- Gini index and Information Gain both measure impurity reduction, but Gini index is based on the probability of misclassifying an instance, while Information Gain is based on the concept of entropy. In general, Gini index tends to be more efficient computationally, while Information Gain can be more accurate in some cases.
- Gain Ratio addresses the bias of Information Gain towards attributes with more distinct values. It normalizes the Information Gain by considering the intrinsic information of the attribute.
- The choice of impurity measure may impact the structure of the resulting decision tree. However, in practice, the choice between Gini index, Information Gain, and Gain Ratio often leads to similar decision trees, and the performance differences are generally small.
It's important to experiment with different impurity measures and evaluate their impact on the performance of the decision tree for a specific dataset or problem.
CART metrics for regression¶
In the case of regression trees, CART uses different metrics to measure the quality of a split. Instead of measuring impurity like in classification, it measures the variation in the target variable. Two common metrics for regression trees are Mean Squared Error (MSE) and Mean Absolute Error (MAE).
We already seen the concept of MSE in the regression course, let's try to code it in a simple way in order to illustrate the difference between MSE and MAE on a simple toy test dataset.
The MAE measures the average absolute difference between the predicted and true target values. Like the MSE, it is calculated as:
$$MAE = (1 / N) * Σ |y_i - y_pred|$$
Let's code this :
def mean_absolute_error(groups):
total_instances = sum([len(group) for group in groups])
mae = 0.0
for group in groups:
group_size = len(group)
if group_size == 0:
continue
group_mean = sum([row[-1] for row in group]) / group_size
group_mae = sum([abs(row[-1] - group_mean) for row in group]) / group_size
mae += group_mae * (group_size / total_instances)
return mae
def mean_squared_error(groups):
total_instances = sum([len(group) for group in groups])
mse = 0.0
for group in groups:
group_size = len(group)
if group_size == 0:
continue
group_mean = sum([row[-1] for row in group]) / group_size
group_mse = sum([(row[-1] - group_mean) ** 2 for row in group]) / group_size
mse += group_mse * (group_size / total_instances)
return mse
#Now, let's consider a toy dataset with two features and a continuous target variable for the MAE illustration
dataset = [
[1, 1, 10],
[1, 2, 12],
[2, 1, 20],
[2, 2, 22],
[3, 1, 30],
[3, 2, 32],
[4, 1, 40],
[4, 2, 42],
]
# Example splits:
# Split 1: [1, 1, 10], [1, 2, 12] | [2, 1, 20], [2, 2, 22], [3, 1, 30], [3, 2, 32], [4, 1, 40], [4, 2, 42]
# Split 2: [1, 1, 10], [1, 2, 12], [2, 1, 20], [2, 2, 22] | [3, 1, 30], [3, 2, 32], [4, 1, 40], [4, 2, 42]
split1 = (dataset[:2], dataset[2:])
split2 = (dataset[:4], dataset[4:])
print("Mean Absolute Error for split 1:", mean_absolute_error(split1))
print("Mean Absolute Error for split 2:", mean_absolute_error(split2))
Mean Absolute Error for split 1: 5.5 Mean Absolute Error for split 2: 5.0
In this example, the second split results in a lower MAE, indicating that it's a better split for the regression problem.
Now, let's create a toy dataset of points and calculate the MAE and MSE for various splits and compare the results.
import numpy as np
import matplotlib.pyplot as plt
# Create a toy dataset
np.random.seed(42)
x = np.linspace(0, 10, 100)
y = 2 * x + 1 + np.random.normal(0, 2, len(x))
dataset = list(zip(x, y))
# Calculate the MAE and MSE for various splits
mae_values = []
mse_values = []
splits = np.arange(1, len(dataset))
for split_idx in splits:
split1 = dataset[:split_idx]
split2 = dataset[split_idx:]
mae_values.append(mean_absolute_error([split1, split2]))
mse_values.append(mean_squared_error([split1, split2]))
# Plot the MAE and MSE values
plt.plot(splits, mae_values, color='blue', label='MAE')
plt.plot(splits, mse_values, color='red', label='MSE')
plt.xlabel('Split Index')
plt.ylabel('Error Value')
plt.legend()
plt.title('MAE vs. MSE for Various Splits')
plt.show()
This code generates a toy dataset of points along a line with some random noise. It then calculates the MAE and MSE for various splits and plots the error values on a single graph with two distinct colors. The graph demonstrates how MAE and MSE values change depending on the chosen split.
The main difference between MAE and MSE is how they penalize large errors. MSE squares the errors, which makes larger errors more prominent in the final error value. In contrast, MAE treats all errors linearly. As a result, MSE is more sensitive to outliers, while MAE is more robust to them.
The choice between MAE and MSE depends on the problem at hand and whether it's more important to penalize large errors or maintain robustness to outliers.
Example on a toy dataset¶
Let's start by coding a small example in order to understand how a tree works in the context of regression: estimating a sine function.
If the word sine reminds you of bad memories of school, know that the sinusoidal functions are far from being abstract notions, they are everywhere in what surrounds us like the movement of waves, the simulation of vibrations to test the resistance of materials and many more things 🤓
Data Simulation¶
For this example, we simulate a sine function with random and independent noises.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
# construisons notre dataset exemple
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
# on ajoute du bruit afin d'avoir de meilleurs données
y[::5] += 3 * (0.5 - rng.rand(16))
The importance of the variation of a hyperparameter in the regression trees¶
As seen previously, here we are looking to estimate our target variable Y (a sine function) with data X 🤓
The first thing we will start with is understanding how a hyperparameter works in the case of a regression tree. A hyperparameter is a parameter whose value is used to control the learning process.
To fully understand this notion, we are going to create 4 regression trees with a different depth (our hyperparameter), respectively 2, 3, 4 and 6. For each of the trees:
- We create the scikit-learn object allowing us to perform a regression on our data with a decision tree
- We optimize (fit) the tree on our data
- We predict (predict) the tree on simulated data
# Fit regression model
regressors = []
depths = [2, 3, 4, 6]
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
Y_test = []
for p in depths:
reg = DecisionTreeRegressor(max_depth=p) # tree creation of deepth p
reg.fit(X, y) # fit the tree on the data
Y_test.append(reg.predict(X_test)) # predict the data
regressors.append(reg)
Finally, we can display the input data and the predicted values for each of our trees.
#plot option
plt.figure(figsize=(16, 10))
colors = [ "darkgray", "cornflowerblue", "yellowgreen", "lightcoral"]
#for loop to print all the trees
for i, reg in zip(range(len(regressors)), regressors):
#define the figure inside the subplot
plt.subplot(220 + i + 1)
plt.plot(X_test, Y_test[i], color=colors[i], label="Profondeur {0}".format(depths[i]), linewidth=2)
#plot the data in the figure
plt.scatter(X, y, s=30, c="darkorange", label="data")
#plot otpions
plt.xlabel("Valeur explicative")
plt.ylabel("Valeur réponse")
plt.title("Visualisation de l'arbre de régression")
plt.legend()
#save the figure
plt.savefig("deep_illustration.png")
plt.show()
More technical details about the CART algorithm¶
We only consider the tree of depth $d=2$. If $d=2$, then there are $3$ splits (or cuts), denoted $t_1, t_2$ and $t_3$. Let's start at the beginning:
Initially, there is no cut. We therefore wonder how to calculate $t_1$, to obtain the rule $X \leq t_1$. To do this, we must introduce a loss metric, that is to say a function that tells us if the cut is good or not. Just like for linear regression, we want to consider the least squares distance between the theoretical value $y$ and the predicted value $\hat{y}$. We therefore want to cut so as to minimize this quadratic loss to the left of $t_1$, but also to the right of $t_1$.
Let's be more formal. Call $R_G = \{ X : X \leq t_1 \}$ the set to the left of $t_1$ and $R_D=\{ X : X > t_1 \}$ the set to the right of $t_1$. It has been said that we want to minimize the quadratic loss, i.e. to solve
$$\min_{t_1 \in \mathbb{R}} \sum_{i=1}^n (y_i-\hat{y})$$
Problem: $t_1$ does not enter the sum! Since this is a split, one must both consider when the point is either in $R_G$ or in $R_D$. Moreover, since we want to assign a weight to each node, which here will define the predicted value $\hat{y}$, we must introduce $c_G$ and $c_D$, which we interpret like this:
- All the points $X$ which belong to $R_G$ (i.e. less than $t_1$) will have the predicted value $c_G$.
- All the points $X$ which belong to $R_D$ (ie strictly greater than $t_1$) will have the predicted value $c_D$.
But these weights must also be optimized in order to be calibrated according to our data. From then on, we obtain a formula much more applicable numerically:
$$\min_{t_1 \in \mathbb{R}} \left(\min_{c_G \in \mathbb{R}} \sum_{x_i \in R_G} (y_i-c_G)^2 +\min_{c_D \ in \mathbb{R}} \sum_{x_i \in R_D} (y_i-c_D)^2 \right)$$
We can simplify the problem as:
$$\min_{t_1 \in \mathbb{R}} \left( \sum_{x_i \in R_G} (y_i-\hat{c_G})^2 + \sum_{x_i \in R_D} (y_i-\hat {c_D})^2 \right)$$
Questions 🤔¶
- Compare the graphs obtained and deduce the role of the depth hyperparameter
max_depth? - Explain the phenomenon of underfitting using the graphs above, for what value of
max_depthour algorithm is underfitting? - Explain the phenomenon of overfitting using the graphs above for what value of
max_depthour algorithm is overfitting? - Finally, what is the best value for the depth hyperparameter
max_depth?
CART cooding from scratch¶
The objective of this project is to build a custom CART Decision Tree Regressor from scratch without relying on external libraries like Scikit-learn 😃
The regressor will be implemented in Python and should be able to handle simple regression tasks.
Project Outline¶
- Understand the CART algorithm and its components.
- Implement the DecisionTreeRegressor class.
- Write functions for splitting the data and calculating the errors.
- Visualize the performance of the custom regressor on a toy dataset.
First let's define a DecisionTreeRegressor class, which has an optional parameter max_depth that determines the maximum depth of the decision tree. If max_depth is not specified, the tree can grow without depth restrictions.
class DecisionTreeRegressor:
def __init__(self, max_depth=None):
self.max_depth = max_depth
Now let's create a Node class. The Node class represents a node in the decision tree. It has a constructor __init__(self, left=None, right=None, value=None, split_feature=None, split_value=None) which initializes the node object with left and right child nodes, the node's value, and the split feature and value (for non-leaf nodes).
class Node:
def __init__(self, left=None, right=None, value=None, split_feature=None, split_value=None):
self.left = left
self.right = right
self.value = value
self.split_feature = split_feature
self.split_value = split_value
Now let's define some important concepts :
- The
fit(self, X, y)takes the input features (X) and the target variable (y) as arguments, and builds the decision tree by calling the _build_tree helper function. - The
predict(self, X)method takes an array of input features (X) and returns the predicted target variable for each input by calling the_predict_singlehelper function. - The
_build_tree(self, X, y, depth)helper function is a recursive function that builds the decision tree by finding the best split for the data and creating child nodes until the stopping criteria (maximum depth) are met. It takes the input features X, target variable y, and the current depth of the tree. If the current depth exceeds max_depth or there is no optimal feature to split on, it creates a leaf node with the mean value of y. Otherwise, it calculates the best feature and value to split the data, creates left and right child nodes, and recurses on both subsets of the data. - The
_find_best_split(self, X, y)helper function finds the best feature and value to split the data on by minimizing the mean squared error (MSE). It iterates through all possible features and split values, calculates the MSE for each split, and returns the best feature and split value that result in the lowest MSE. - The
_predict_single(self, x)helper function takes a single input feature vector x and predicts the target variable for it. It traverses the decision tree from the root, following the left or right child nodes based on the split feature and value, until it reaches a leaf node. The value of the leaf node is the predicted target variable.
#entier code
import numpy as np
# Define the main DecisionTreeRegressor class
class DecisionTreeRegressor:
# Class constructor with an optional parameter `max_depth` for the maximum depth of the tree
def __init__(self, max_depth=None):
self.max_depth = max_depth
# Define the inner Node class representing a node in the decision tree
class Node:
# Node class constructor with parameters for the left and right child nodes, value, split feature, and split value
def __init__(self, left=None, right=None, value=None, split_feature=None, split_value=None):
self.left = left
self.right = right
self.value = value
self.split_feature = split_feature
self.split_value = split_value
# `fit` method takes the input features (X) and target variable (y) and builds the decision tree
def fit(self, X, y):
self.root = self._build_tree(X, y, 0)
# `predict` method takes input features (X) and returns predictions for each input
def predict(self, X):
return [self._predict_single(x) for x in X]
# Recursive helper function `_build_tree` for building the decision tree
def _build_tree(self, X, y, depth):
if len(y) == 0:
return None
if self.max_depth is not None and depth >= self.max_depth:
return self.Node(value=np.mean(y))
split_feature, split_value = self._find_best_split(X, y)
if split_feature is None:
return self.Node(value=np.mean(y))
left_mask = X[:, split_feature] <= split_value
right_mask = ~left_mask
left_node = self._build_tree(X[left_mask], y[left_mask], depth + 1)
right_node = self._build_tree(X[right_mask], y[right_mask], depth + 1)
return self.Node(left=left_node, right=right_node, split_feature=split_feature, split_value=split_value)
# Helper function `_find_best_split` to find the best feature and value to split the data
def _find_best_split(self, X, y):
best_mse = float("inf")
best_split_feature = None
best_split_value = None
for feature in range(X.shape[1]):
feature_values = X[:, feature]
for value in feature_values:
left_mask = feature_values <= value
right_mask = ~left_mask
left_y = y[left_mask]
right_y = y[right_mask]
if len(left_y) <= 1 or len(right_y) <= 1:
continue
mse = len(left_y) * np.var(left_y) + len(right_y) * np.var(right_y)
if mse < best_mse:
best_mse = mse
best_split_feature = feature
best_split_value = value
return best_split_feature, best_split_value
# Helper function `_predict_single` for predicting the target variable for a single input feature vector
def _predict_single(self, x):
node = self.root
while node.left is not None and node.right is not None:
if x[node.split_feature] <= node.split_value:
node = node.left
else:
node = node.right
return node.value
Now let's generate our toy sample dataset then apply our DecisionTreeRegressor class :
import matplotlib.pyplot as plt
np.random.seed(42)
X = np.linspace(0, 10, 100)[:, np.newaxis]
y = 2 * X.ravel() + 1 + np.random.normal(0, 2, len(X))
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
regressors = []
depths = [2, 3, 4, 6]
Y_test = []
for p in depths:
reg = DecisionTreeRegressor(max_depth=p)
reg.fit(X, y)
Y_test.append(reg.predict(X_test))
regressors.append(reg)
plt.figure(figsize=(16, 10))
colors = ["darkgray", "cornflowerblue", "yellowgreen", "lightcoral"]
# for loop to print all the trees
for i, reg in zip(range(len(regressors)), regressors):
# define the figure inside the subplot
plt.subplot(220 + i + 1)
plt.plot(X_test, Y_test[i], color=colors[i], label="Deep: {0}".format(depths[i]), linewidth=2)
# plot the data in the figure
plt.scatter(X, y, s=30, c="darkorange", label="data")
# plot options
plt.xlabel("Feature")
plt.ylabel("Target")
plt.title("Tree visualization")
plt.legend()
# save the figure
plt.savefig("deep_illustration.png")
plt.show()