Fundamentals of Audio Processing: Sound, Waveforms, and Frequency

Introduction to Sound

Sound is a type of energy that is produced by vibrating objects. The vibrations cause air molecules around the object to move, creating pressure waves that we can hear. Sound can travel through different mediums such as air, water, and solids an variate its propriety.

Mathematical Representation

No direct mathematical equation is involved in this definition, but it's important to understand that sound propagation can be modeled using wave equations.

The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves), more on wikipedia

In this course we will be focusing on mechanical wave not other type of waves (like electromagnetics wave).

A mechanical wave is a disturbance that travels through a medium, transferring energy from one point to another. Sound is a mechanical wave that requires a medium (like air, water, or solid) to travel.

The Wave Equation

The general wave equation for a wave traveling through a medium in one dimension is given by:

\[\frac{\partial^2 u}{\partial t^2} = v^2 \frac{\partial^2 u}{\partial x^2}\]

Where:

\(u\) represents the wave function, indicating the displacement of the medium at position \(x\) and time \(t\).
\(v\) is the velocity of the wave in the medium.
\(\frac{\partial^2 u}{\partial t^2}\) is the second partial derivative of \(u\) with respect to time, indicating acceleration.
\(\frac{\partial^2 u}{\partial x^2}\) is the second partial derivative of \(u\) with respect to position, indicating curvature of the wave.

Understanding Waveforms

Enought complexe mathematics representation let's talk about something more concrete : Visualizing sound with waveforms.

A waveform is a visual representation of the variation in air pressure caused by sound over time. It can be plotted as pressure vs. time, showing how the pressure changes due to the vibration of the sound source. We use sin(x) and cos(x) functions to represent this waves.

Simple Sine Wave Equation

A simple sine wave, which we can call a pure tone, can be described mathematically as:

\[ p(t) = A \sin(2 \pi f t + \phi)\]

Where:

\(p(t)\) is the pressure variation as a function of time.
\(A\) is the amplitude of the wave, representing the maximum pressure variation.
\(f\) is the frequency of the wave, representing how many cycles occur in one second.
\(t\) is time. \(\phi\) is the phase of the wave, representing the shift of the wave in time.
\(2πf\) is the angular frequency of the wave.

You can play on this excellent website here and clique on the magnify glass to see the waves form when you touch piano notes 🎹

Complex Sounds and Waveforms

In every day life we do not often have simple weve forme like the one above, it's more complex.

Complex sounds are made up of multiple sine waves with different frequencies, amplitudes, and phases. Since it is a lot of waves (informations) these can be analyzed using Fourier analysis to understand the sound's spectrum.

Fourier Transform Equation

The Fourier Transform allows us to decompose a complex waveform into its constituent sine waves with the formula below :

\[F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt\]

Where:

\(F(ω)\) is the Fourier transform of \(f(t)\), representing the frequency spectrum of the waveform.
\(f(t)\) is the time-domain signal (the complex waveform).
\(ω\) is the angular frequency (\(2π\) times the frequency).
\(e^{−iωt}\) is the complex exponential function, where \(i\) is the complex imaginary unit.

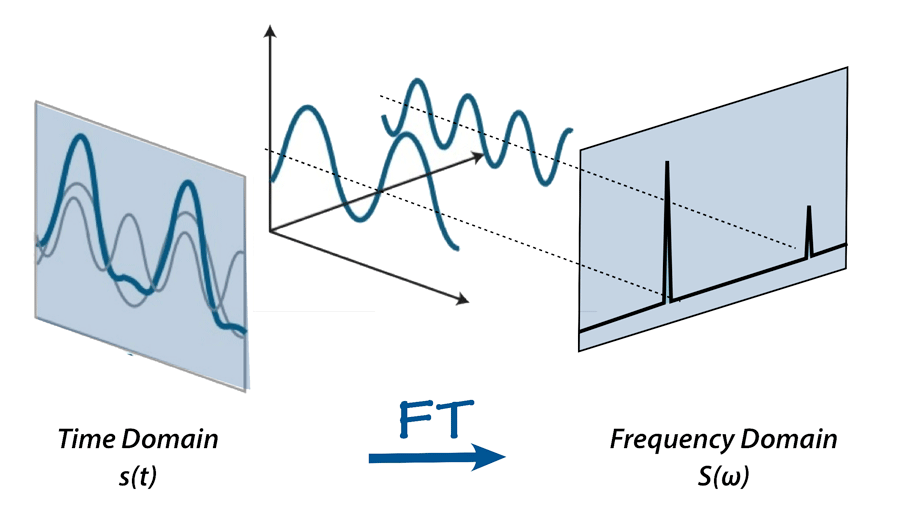
This illustration is based on the excellent medium article The Fourier Transform and its Application in Machine Learning who is explain very well the difference between Continuous Fourier Transform (CFT) and the Discrete Fourier Transform (DFT) and their applications in signal processing.

These equations and concepts provide a mathematical foundation for understanding sound and waveforms, essential for diving deeper into audio processing.

Sound Properties and Their Perception

We classified two categories of sounds : Periodic and Aperiodic.

Periodic Sounds: These are sounds where the wave pattern repeats at regular intervals, called the period. The simplest form of a periodic sound is a pure tone (like we have seen earlier), represented by a sine wave.
Aperiodic Sounds: These sounds do not have a repeating pattern. Noise and transient sounds are examples of aperiodic sounds.

For aperiodic sounds, no simple mathematical model can describe their complexity, as their waveforms do not repeat and can be quite random.

The Physics behind Sound Waves

Earlier we talked about Amplitude, Frequency, and Phase but let's take two seconds and focus on the phisics behind the scene.

Amplitude \(A\): Represents the maximum displacement of the wave from its rest position, directly related to the sound's loudness (aka what's you ear 🔉).
Frequency \(f\): The number of oscillations per second of the wave, measured in Hertz (Hz). It determines the pitch of the sound.
Phase \(φ\): The initial angle of the wave at \(t=0\). It determines the starting point of the wave cycle.

Amplitude and Loudness

The loudness of a sound is proportional to the square of the amplitude of the wave:

\[L \propto A^2\]

Where, \(L\) is the loudness and \(A\) is the amplitude.

Frequency and Pitch

The frequency of a sound wave is inversely related to its period (the duration of one cycle), given by:

\[f = \frac{1}{T}\]

The pitch of a sound is directly related to its frequency, but the human perception of pitch is logarithmic:

\[\text{Pitch} \propto \log(f)\]

Pitch Perception and Its Logarithmic Nature

Pitch is how we perceive the frequency of a sound, which is not a linear relationship but a logarithmic one. This means that equal ratios of frequencies are perceived as equal intervals in pitch.

The relationship between frequency and pitch can be expressed using the logarithmic scale of music, where the octave is divided into 12 semitones (equal temperament tuning):

\[\text{Pitch} = 69 + 12 \times \log_2\left(\frac{f}{440 \, \text{Hz}}\right)\]

Where :

\(Pitch\) is the MIDI note number.
\(f\) is the frequency of the note.
\(440 Hz\) is the reference frequency of the note A4, the standard tuning pitch. For your culture when you see someone tune a piano with a little metalic tool is for the sound of the A4 🤓

Phase and Waveform Alignment

The phase determines the waveform's position at a given point in time. Two simple periodic waves with the same frequency and amplitude but different phases will align differently:

\[\begin{cases} p_1(t) = A \sin(2 \pi f t + \phi_1)\\ p_2(t) = A \sin(2 \pi f t + \phi_2) \end{cases} \]

The difference in phase \(Δϕ=ϕ_2 - ϕ_2\) will determine the relative alignment of \(p_1(t)\) and \(p_2(t)\).

MIDI Notes and Frequency Mapping

MIDI for Musical Instrument Digital Interface uses a standardized numbering system to represent pitches. It's like the ASCII convention for the musics guys 🎹. For example Middle C is assigned the MIDI note number 60.

The frequency of a MIDI note can be calculated as:

\[f = 440 \times 2^{\frac{n-69}{12}}\]

Where:

\(f\) is the frequency in Hertz.
\(n\) is the MIDI note number.

This equation shows how to convert a MIDI note number into its corresponding frequency, allowing for the synthesis of musical tones or the analysis of musical pieces.

Advanced Concepts in Sound Analysis

Overview of Audio Processing in Machine Learning

Audio processing involves techniques for analyzing, altering, or synthesizing audio signals. Machine learning applications in audio processing include speech recognition, music recommendation, sound classification and even music generation 🧞‍♂️

Key Concepts and Mathematical Tools

Fourier Transform

Fundamental for converting time-domain signals into frequency-domain representation like we have seen earlier.

Spectrogram

A visual representation of the spectrum of frequencies in a sound or other signal as they vary with time.

Generated using the Short-Time Fourier Transform (STFT), which is a sequence of Fourier transforms of windowed signal segments. STFT Equation:

\[STFT\{x(t)\}(f, \tau) = \int_{-\infty}^{\infty} x(t) w(t-\tau) e^{-i 2\pi f t} dt\]

Where, \(w(t)\) is the window function, \(f\) is frequency, and \(τ\) is the time around which the window is centered.

Sound Intensity \(I\) and Loudness \(L\)

The sound intensity is calculated as :

\[I = \frac{P}{A}\]

Where \(P\) is the acoustic power in Watts, and \(A\) is the area in square meters through which the power is distributed.

Related to intensity, but perceived loudness also depends on frequency. Approximated by the equation:

\[L = K \log_{10}(I/I_0)\]

Where \(L\) is the loudness level in decibels (dB), \(I\) is the sound intensity, \(I_0\) is the reference intensity (typically \(10^{−12} W/m²\)), and \(K\) is a constant that depends on the context (often set to 10 for sound in air).

Below a table of differents sound intensity level for us humain 🤓

This table is from the article about Sound intensity level, Beats and Doppler Effect if you want to now more about Doppler effect and the sound barrier 🚀

Harmonic Analysis for Timbre

A sound's timbre can be analyzed by examining its harmonic content using the Fourier series to represent the sound wave:

\[f(t) = A_0 + \sum_{n=1}^{\infty} [A_n \cos(n \omega_0 t) + B_n \sin(n \omega_0 t)]\]

Where \(A_0\) is the average value of the function, \(A_n\) and \(B_n\) are the amplitudes of the cosine and sine components at the \(n^{th}\) harmonic, and \(ω_0\) is the fundamental angular frequency.

That's why piano and violin do not have the same effect on your ears even they play the same note (same frequency and amplitude), as you can see below they are indeed very different :

Enought theory let's code a little in order to unerstand all this concepts 😎