Recursive Algorithms¶
In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.
A common algorithm design tactic is to divide a problem into sub-problems of the same type as the original, solve those sub-problems, and combine the results. This is often referred to as the divide-and-conquer method. More informations on wikipedia here)
Basic example : Fibonacci sequence¶
The Fibonacci sequence is a sequence of integers, starting with 0 and 1, in which each element is the sum of the previous two numbers. The first 10 Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34. The mathematical definition of the Fibonacci sequence is given by the following recurrence relation:
$$F_n = F_{n-1} + F_{n-2}$$
where $F_0 = 0$ and $F_1 = 1$
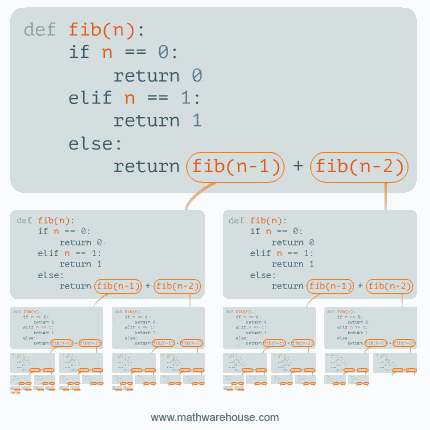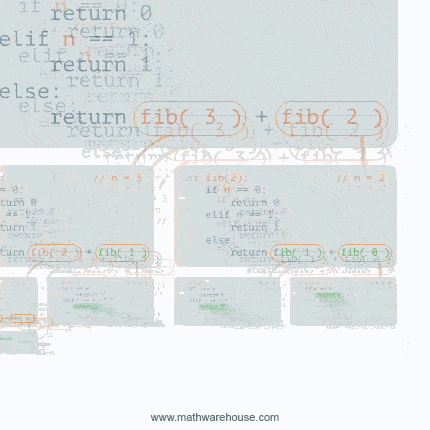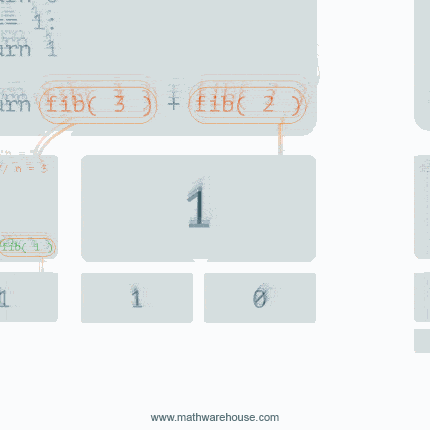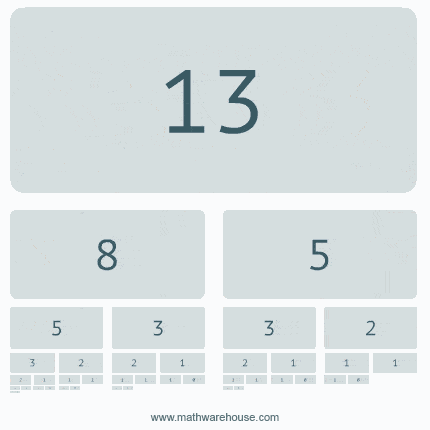
The Fibonacci sequence is a good example of a recursive algorithm because the value of the sequence at a given index depends on the values of the previous two indices. The recursive solution to this problem is to calculate the value of the sequence at a given index by summing the values of the sequence at the previous two indices. The base case for this recursive solution is when the index is 0 or 1, in which case the value of the sequence is 0 or 1, respectively.
def fibo(n):
if n==0:
return 0
elif n==1:
return 1
else:
# if you want to see the process of recursion, uncomment the following line
#print(f'call : fibo({n-1}) and fibo({n-2})')
return fibo(n-1)+fibo(n-2)
%time
fibo(21)
CPU times: user 4 µs, sys: 0 ns, total: 4 µs Wall time: 7.63 µs
10946
The Sum of Digits example¶
You're given a non-negative integer. You want to find the sum of its digits.
Write a recursive function call sum_of_digits(n: int) -> int that returns the sum of the digits of the number n.
Input: 1234
Output: 10 (because 1 + 2 + 3 + 4 = 10)
def sum_of_digits(n: int) -> int:
if n == 0:
return 0
else:
return n % 10 + sum_of_digits(n // 10)
sum_of_digits(1234)
10
Palindrome example¶
You're given a string. You want to reverse its characters.
Write a recursive function Palindrome(s: str) -> bool that true if the string is a palindrome, false otherwise. You should write an intermediaire function reverse_string(s: str) -> str that use recursion and reverse the string.
Input: "hello"
Output: False
Input: "kayak"
Output: True
def reverse_string(s: str) -> str:
if len(s) == 0:
return s
else:
return s[-1] + reverse_string(s[:-1])
def palindrome(s: str) -> bool:
if len(s) == 0:
return False
else:
pal = s[-1] + reverse_string(s[:-1])
if pal == s:
return True
return False
palindrome('kayak')
True
Optimizing recursive algorithms : memoization¶
Like you have seen in the previous gif calling a recursive function can be very expensive in terms of memory and time. In fact, the recursive function will call itself until it reaches the base case. In the case of the Fibonacci sequence, the recursive function will call itself $n$ times to calculate the $n^{th}$ number of the sequence. This is a very inefficient way to calculate the Fibonacci sequence.
We remember that in terme of complexity, the recursive function will have a complexity of $O(2^n)$ which is very bad. But we know also that we can store the result of the previous call to avoid to call the function again. This is called memoization.

Memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again. More details on Wikipedia here or in this article from Geeksforgeeks
Let's take a look at the example of Fibonacci sequence. We can store the result of the previous call in a dictionary and check if the result is already in the dictionary before calling the function again 🤓
#optimal solution with a hashmap to store the values
def optimizeFibo(n):
fiboMap = {0:0, 1:1}
if n in fiboMap:
return fiboMap[n]
else:
fiboMap[n] = optimizeFibo(n-1)+optimizeFibo(n-2)
return fiboMap[n]
%time
optimizeFibo(21)
CPU times: user 1e+03 ns, sys: 0 ns, total: 1e+03 ns Wall time: 1.67 µs
10946