Divide and Conquer Algorithms¶

Divide and Conquer is a recursive problem-solving approach that divides a problem into smaller subproblems until the subproblems become simple enough to be solved directly. The solutions to the subproblems are then combined to give a solution to the original problem. Like we have said in the introduction, imagine you have a huge puzzle to solve. Instead of trying to solve the whole thing at once, you divide it into smaller parts, solve each part, and then put them all together. That's what these algorithms do.

Divide and conquer is a potent algorithmic strategy employed to address a wide range of significant challenges. In everyday life, humans instinctively apply this approach for tasks such as organizing a deck of cards or searching for a contact in a directory.

The divide and conquer methodology operates in three phases:

1. Breaking the problem into smaller chunks
2. Addressing these chunks
3. Combine the solutions to resolve the primary issue

Typically, this strategy incorporates a recursive element where the smaller chunks are tackled. Additionally, there's a foundational scenario, or a base case, where the problem can no longer be subdivided.

Incorporating this strategy offers the advantage of reduced time complexity, making algorithms more efficient. By breaking problems down and tackling them in parts, we can often achieve faster and more optimized solutions, especially for large datasets. This efficiency is one of the primary reasons why divide and conquer is a cornerstone in algorithmic design.

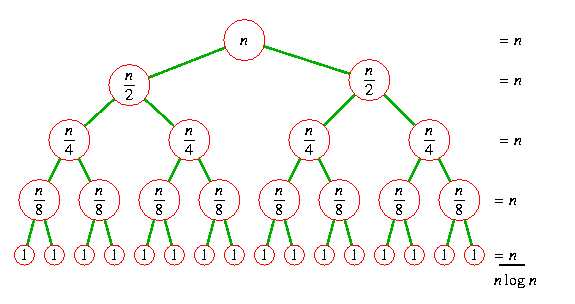
We have seen some of the divide and conquer algorithms in the previous chapters like merge sort, quick sort, and binary search 🤓

Implementing the Cooley–Tukey FFT Algorithm¶

The Discrete Fourier Transform (DFT) is a fundamental operation in signal processing and telecommunications. The Cooley–Tukey FFT algorithm offers an efficient way to compute the DFT more efficiently than the straightforward evaluation of the DFT's definition. You can find more about the algorithm here.

Before diving into the solution, let's understand the divide and conquer procedure in the Cooley–Tukey FFT algorithm:

1. Divide: Split the input sequence into even and odd indexed elements.
2. Conquer: Recursively compute the FFT of these smaller sequences.
3. Combine: Combine the results of the smaller FFTs into the FFT of the original sequence using a formula derived from the DFT definition.

Now, let's implement the Cooley–Tukey FFT algorithm in Python 🐍 with the following example input/output:

Input: [1, 1, 1, 1]
Output: [(4+0j), 0j, (0+0j), 0j]

In [34]:

import cmath

def FFT(x):
    N = len(x)
    if N <= 1:
        return x

    # Divide 
    even = FFT(x[0::2])
    odd = FFT(x[1::2])

    # Combine
    T = [cmath.exp(-2j * cmath.pi * k / N) * odd[k] for k in range(N // 2)]
    return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]

# Test
sequence = [1, 1, 1, 1]
print(FFT(sequence))

import cmath def FFT(x): N = len(x) if N <= 1: return x # Divide even = FFT(x[0::2]) odd = FFT(x[1::2]) # Combine T = [cmath.exp(-2j * cmath.pi * k / N) * odd[k] for k in range(N // 2)] return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)] # Test sequence = [1, 1, 1, 1] print(FFT(sequence))

[(4+0j), 0j, 0j, 0j]

The Cooley–Tukey FFT algorithm significantly reduces the computational complexity of the DFT from $O(n^2)$ to $O(nlog(n))$ making it much more efficient for large sequences.

This divide and conquer approach is what allows the FFT to be so efficient. By breaking the problem down into smaller parts and using the properties of the DFT, the Cooley–Tukey algorithm can compute the DFT in much fewer operations than a direct computation.

More Divide and Conquer Algorithms¶

You can find more divide and conquer algorithms on Geeksforgeeks website here that cover pretty much all the well known algorithms in this category.